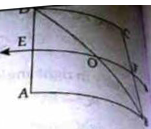
In a trapezium ABCD, AB is parallel to CD. If E is midpoint of side AD and a line drawn from point E, parallel to the parallel sides cuts BC at F then
BF = CF if AD = BC
BF = CF ia always true
BF:CF is less than 1 if AD<BC
BF:CF is greater than 1 if AD>BC
The correct Answer is:B
Step by step video, text & image solution for In a trapezium ABCD, AB is parallel to CD. If E is midpoint of side AD and a line drawn from point E, parallel to the parallel sides cuts BC at F then by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B5videos
LINES AND ANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B10videos
TRIGONOMETRIC RATIO OF SPECIFIC ANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of the above - Question 2 - Select One
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
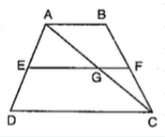
In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
 View Solution
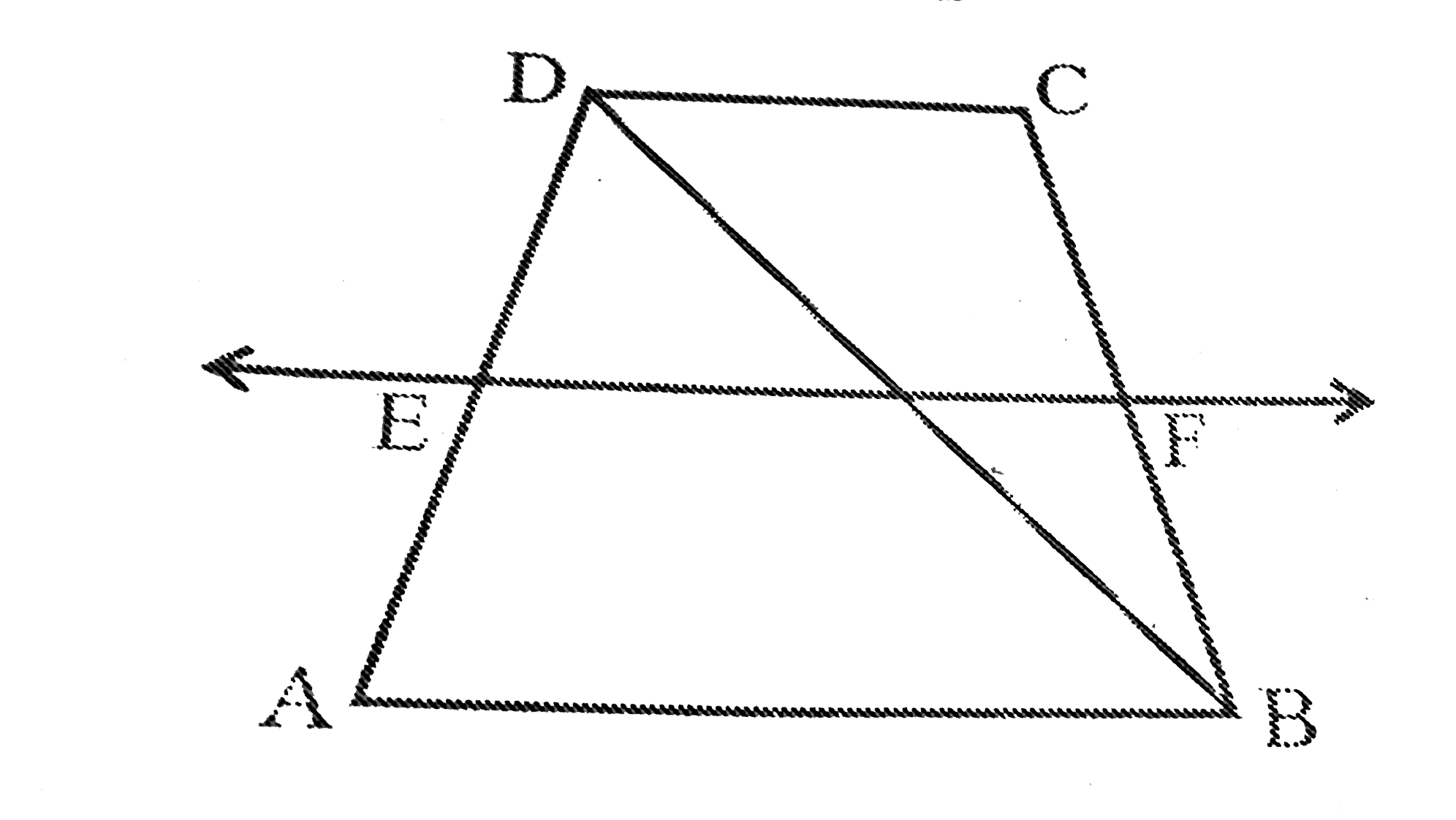
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
 View Solution
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionThe line joining the mid points of the diagonals of a trapezium is parallel to each of the parallel sides and equal to half of their difference
View SolutionThe line drawn from the midpoint of one side of a triangle parallel to another side bisects the third side.
View Solution