ABCD is a parallelogram. E is a point on extended side AB such that AB = BE. By joining D to E it intersects side BC at P. Find length of PC if BC = 15 cm.
The correct Answer is:7.5
To solve the problem step by step, we will use the properties of a parallelogram and the midpoint theorem.
Step 1: Understand the Geometry
We have a parallelogram ABCD, where E is a point on the extended line of AB such that AB = BE. This means that E is twice the distance from A to B.
Step 2: Identify the Midpoint
Since E is on the extended line of AB and AB = BE, we can conclude that B is the midpoint of AE. Therefore, we can denote:
- AE = AB + BE = 2 * AB
Step 3: Apply the Midpoint Theorem
In triangle AED, by the midpoint theorem, we know that if B is the midpoint of AE, then:
BP=12AD
This is because AD is parallel to BP and BC.
Step 4: Relate AD and BC
Since ABCD is a parallelogram, we know that:
AD=BC
Thus, we can substitute BC for AD in our earlier equation:
BP=12BC
Step 5: Substitute the Value of BC
We are given that:
BC=15cm
Substituting this value into the equation gives us:
BP=12×15=7.5cm
Step 6: Find Length of PC
Since P divides BC into two segments, we can find PC by subtracting BP from BC:
PC=BC−BP
PC=15−7.5=7.5cm
Final Answer
The length of PC is:
PC=7.5cm
---
We have a parallelogram ABCD, where E is a point on the extended line of AB such that AB = BE. This means that E is twice the distance from A to B.
Since E is on the extended line of AB and AB = BE, we can conclude that B is the midpoint of AE. Therefore, we can denote:
- AE = AB + BE = 2 * AB
In triangle AED, by the midpoint theorem, we know that if B is the midpoint of AE, then:
BP=12AD
This is because AD is parallel to BP and BC.
Since ABCD is a parallelogram, we know that:
AD=BC
Thus, we can substitute BC for AD in our earlier equation:
BP=12BC
We are given that:
BC=15cm
Substituting this value into the equation gives us:
BP=12×15=7.5cm
Since P divides BC into two segments, we can find PC by subtracting BP from BC:
PC=BC−BP
PC=15−7.5=7.5cm
The length of PC is:
PC=7.5cm
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - QUADRILATERALEXERCISE - EXERCISE48videos
QUADRILATERAL
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PROFIT & LOSSEXERCISE - Questions200videos
PROFIT & LOSS
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - RATIO & PROPORTIONEXERCISE - QUESTIONS113videos
RATIO & PROPORTION
Similar Questions
Knowledge Check
- Question 1 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC - Question 2 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1 - Question 3 - Select One
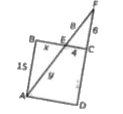
In the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
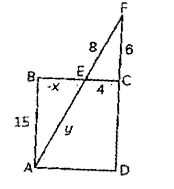
Perimeter of ΔABE=A35cmB36cmC40cmD45cm
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
 View Solution
View Solution□ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.
 View Solution
View Solution□ABCD is a parallelogram. Point E is on side BC. Line DE intersects ray AB in point T. Prove that DE×BE=CE×TE.
View Solution

