Question

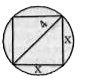
If a square is inscribed in a circle whose area is 314 sq. cm, then the length of each side of the square is

Options

A. `5 sqrt2` cm
B. `20 sqrt2` cm
C. 10 cm
D. `10 sqrt2` cm

Answer

D

Explanation

To find the length of each side of a square inscribed in a circle with an area of 314 sq. cm, we can follow these steps:

1. Understand the relationship between the circle and the square:
- A square inscribed in a circle means that all four corners of the square touch the circle. The circle is called the circumcircle of the square.

2. Use the area of the circle to find the radius:
- The area \( A \) of the circle is given by the formula:
\( A = \pi r^2 \)
- We know the area is 314 sq. cm, so we can set up the equation:
\( \pi r^2 = 314 \)

3. Solve for \( r^2 \):
- Rearranging the equation gives:
\( r^2 = \frac{314}{\pi} \)
- Using \( \pi \approx 3.14 \):
\( r^2 = \frac{314}{3.14} \approx 100 \)

4. Calculate the radius \( r \):
- Taking the square root of both sides gives:
\( r = \sqrt{100} = 10 \text{ cm} \)

5. Relate the radius to the side of the square:
- The diagonal \( d \) of the square is equal to the diameter of the circle. Since the diameter \( D \) is twice the radius:
\( D = 2r = 2 \times 10 = 20 \text{ cm} \)
- The diagonal \( d \) of the square can also be expressed in terms of the side length \( s \) of the square using the formula:
\( d = s\sqrt{2} \)

6. Set the two expressions for the diagonal equal:
- Therefore, we have:
\( s\sqrt{2} = 20 \)

7. Solve for the side length \( s \):
- Dividing both sides by \( \sqrt{2} \):
\( s = \frac{20}{\sqrt{2}} = 20 \times \frac{\sqrt{2}}{2} = 10\sqrt{2} \text{ cm} \)

Final Answer:
The length of each side of the square is \( 10\sqrt{2} \) cm.

---