BC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of ∠BAC+∠OBC ?
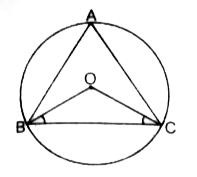
120∘
60∘
90∘
180∘
The correct Answer is:C
Step by step video, text & image solution for BC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of angle BAC + angle OBC ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8A71videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
AC is a chord of that circle whose center is 'O'. If B is any point on arc AC and ∠OCA=20∘, then what is the measurement of ∠ABC ?
A100∘B40∘C140∘D110∘ - Question 2 - Select One
In the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD
 A90∘B80∘C45∘D60∘
A90∘B80∘C45∘D60∘ - Question 3 - Select One
In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
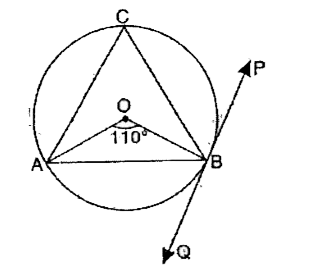 A45∘B70∘C55∘D35∘
A45∘B70∘C55∘D35∘
In the figure, BC is a chord of the circle with centre o and A is a point on the minor are BC. Then ∠ABC−∠OBCis equal to
View SolutionAC=25 and D is a point on BC such that AD is the bisector of angle A, as shown in the figure. What is the length of AD?
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
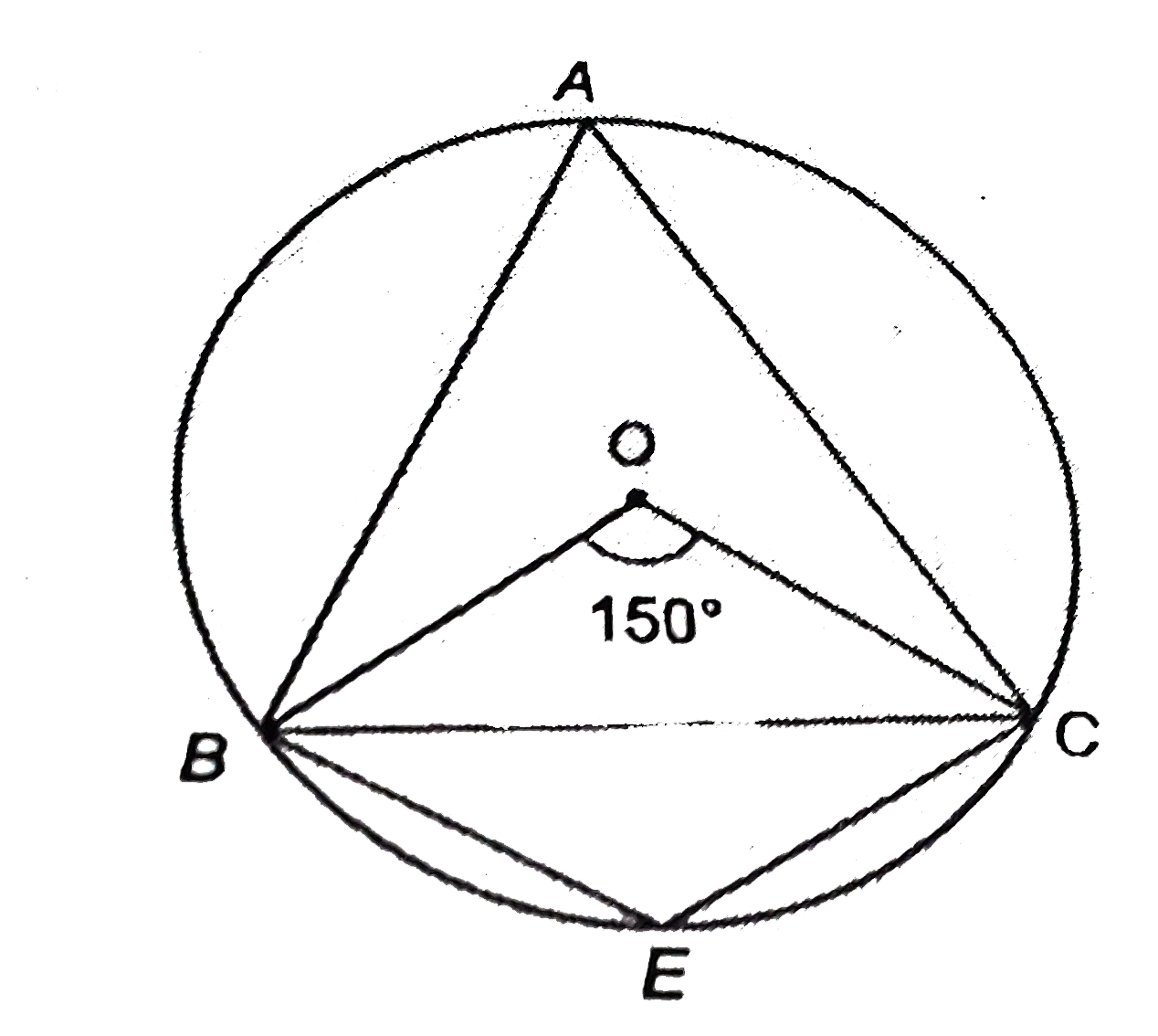 View Solution
View SolutionAB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
View SolutionAlloy A contains 40% gold and 60% silver. Alloy B contains 35% gold and 40% silver and 25% copper. Alloys A and B are mixed in the ratio of 1:4 .What is the ratio of gold and silver in the newly formed alloy is?
View Solution

