A body is moving unidirectionally under the influence of a sources of constant power. The square of its displacement in time t is proportional to
t
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the displacement of a body moving under constant power and time. The key points to consider are the definitions of power, work, and kinetic energy.
1. Understanding Power:
Power (P) is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where W is the work done and t is the time taken.
2. Work Done:
The work done by the body can be expressed in terms of kinetic energy. According to the work-energy theorem:
W=ΔKE=12mv2
where m is the mass of the body and v is its velocity.
3. Relating Work and Power:
Since power is constant, we can express work done over time as:
W=P⋅t
Setting the two expressions for work equal gives:
P⋅t=12mv2
4. Solving for Velocity:
Rearranging the equation to find v2:
v2=2Ptm
5. Relating Velocity to Displacement:
Velocity is also defined as the rate of change of displacement:
v=dsdt
Substituting for v in terms of displacement gives:
dsdt=√2Ptm
6. Separating Variables:
To find displacement s, we can separate variables:
ds=√2Pm⋅t1/2dt
7. Integrating:
Integrating both sides:
s=∫√2Pm⋅t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2+C
where C is the constant of integration.
8. Finding the Square of Displacement:
The square of displacement s2 is then proportional to t3:
s2∝t3
Conclusion:
The square of the displacement of the body in time t is proportional to t3.
Power (P) is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where W is the work done and t is the time taken.
The work done by the body can be expressed in terms of kinetic energy. According to the work-energy theorem:
W=ΔKE=12mv2
where m is the mass of the body and v is its velocity.
Since power is constant, we can express work done over time as:
W=P⋅t
Setting the two expressions for work equal gives:
P⋅t=12mv2
Rearranging the equation to find v2:
v2=2Ptm
Velocity is also defined as the rate of change of displacement:
v=dsdt
Substituting for v in terms of displacement gives:
dsdt=√2Ptm
To find displacement s, we can separate variables:
ds=√2Pm⋅t1/2dt
Integrating both sides:
s=∫√2Pm⋅t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2+C
where C is the constant of integration.
The square of displacement s2 is then proportional to t3:
s2∝t3
The square of the displacement of the body in time t is proportional to t3.
Topper's Solved these Questions
Similar Questions
A body is moving undirectionally under the influence of a source of constatn power. It displacement in time t is proportional to (i) t1/2 (ii) t (iii) t3/2 (iv) t2
View SolutionA body undergoing a straight line motion is under the influence of source of constant power. How does its displacement very with time?
View Solution
Knowledge Check
- Question 1 - Select One
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A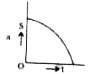 B
B C
C D
D
- Question 2 - Select One
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A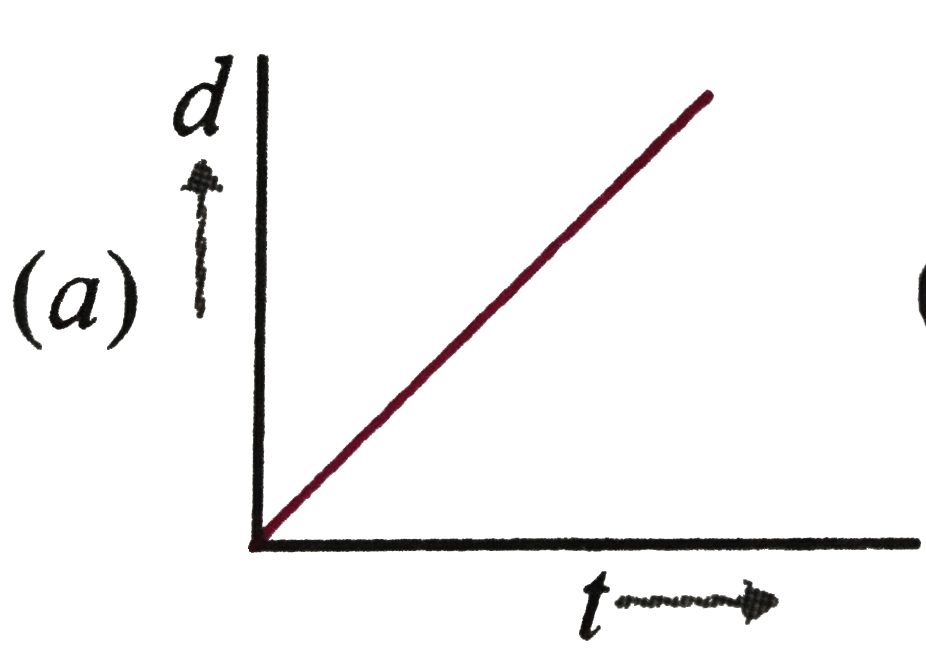 B
B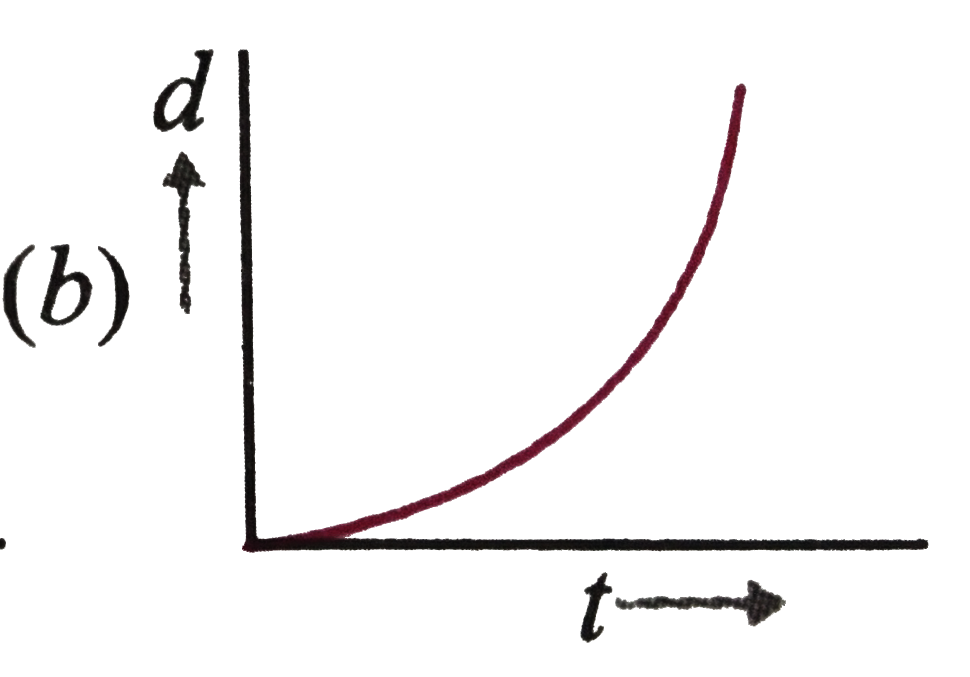 C
C D
D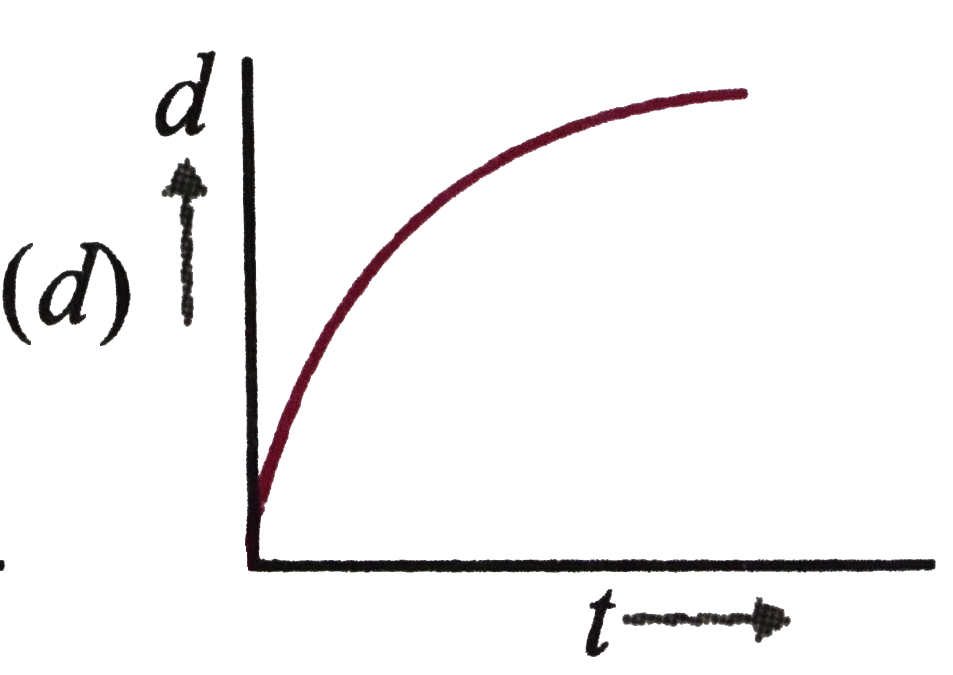
- Question 3 - Select One
A body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
At1/2BtCt3/2Dt2
A body is under the influence of a force such that it delivers a constant power p. The variation of position with time of body as
View SolutionA body at rest is moved along a horizontal straight line by a machine delivering a constant power. The distance moved by the body in time ‘t’ is proportional to:
View SolutionA body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body in time t is proportional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View Solution

