Statement - I : Let the side DE of a triangle
DEF be divided at S so that
DSDE=1√2 . If a line through
S parallel to EF meets DF at
T, then the area of triangle
DEF is twice the area of the
triangle DST.
Statement - II : The areas of the similar
triangles are proportional to
the squares on the
corresponding sides.
Which one of the following is correct in
respect of the above statements ?
Both statement - I and statement-II are
true and statement -II is the correct
explanation of statement - I
Both statement-I and statement - II are
true but statement - II is not the correct
explanation of statement - I
Statement - I is true, but statement -II is false
Statement - II is true, but statement - I is false
To solve the problem, we need to analyze the given statements and apply the properties of triangles and their areas.
1. Understanding the Triangle and the Given Ratio:
- We have a triangle DEF with a point S on side DE such that DSDE=1√2.
- This implies that DS=DE√2.
Hint: Remember that the ratio of segments on a line can help us understand the proportions in the triangle.
2. Finding the Ratio of DE to DS:
- Since DSDE=1√2, we can find DEDS by taking the reciprocal:
DEDS=√2
Hint: The reciprocal of a ratio gives you the inverse relationship between the segments.
3. Using the Property of Parallel Lines:
- Since line ST is drawn parallel to EF, by the Basic Proportionality Theorem (or Thales' theorem), we know that the areas of triangles formed by a transversal line intersecting two parallel lines are proportional to the squares of the corresponding sides.
- Therefore, we can write:
Area(DEF)Area(DST)=(DEDS)2
Hint: Recall that when two triangles share a vertex and have their bases on parallel lines, their areas are proportional to the squares of their corresponding sides.
4. Substituting the Ratio:
- We have already found DEDS=√2. Now we can substitute this into the area ratio:
Area(DEF)Area(DST)=(√2)2=2
Hint: Squaring the ratio gives you the relationship between the areas of the triangles.
5. Conclusion about the Statements:
- From the calculations, we see that the area of triangle DEF is indeed twice the area of triangle DST, which confirms Statement I.
- Statement II is also true, as it states that the areas of similar triangles are proportional to the squares of their corresponding sides, which we used in our derivation.
Hint: Verify the logical flow of statements to ensure that they support each other.
Final Answer:
Both statements are true, and Statement II is the correct explanation for Statement I.
- We have a triangle DEF with a point S on side DE such that DSDE=1√2.
- This implies that DS=DE√2.
- Since DSDE=1√2, we can find DEDS by taking the reciprocal:
DEDS=√2
- Since line ST is drawn parallel to EF, by the Basic Proportionality Theorem (or Thales' theorem), we know that the areas of triangles formed by a transversal line intersecting two parallel lines are proportional to the squares of the corresponding sides.
- Therefore, we can write:
Area(DEF)Area(DST)=(DEDS)2
- We have already found DEDS=√2. Now we can substitute this into the area ratio:
Area(DEF)Area(DST)=(√2)2=2
- From the calculations, we see that the area of triangle DEF is indeed twice the area of triangle DST, which confirms Statement I.
- Statement II is also true, as it states that the areas of similar triangles are proportional to the squares of their corresponding sides, which we used in our derivation.
Both statements are true, and Statement II is the correct explanation for Statement I.
Similar Questions
Let Δ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
View SolutionIn the triangle ABC, the base BC is trisected
at D and E. The line through D, parallel to
AB, meets AC at F and the line through E
parallel to AC meets AB at G. Let EG and
DF intersect at H. What is the ratio of the
sum of the area of parallelogram AGHF and
the area of the triangle DHE to the area of
the triangle ABC ?
View Solution
Knowledge Check
Statement- 1: If the sines of the angles of a triangle are in A.P., then the altitudes ef the triangle are also in A.P.
Statement-2: Twice the area of a triangle is equal to the product of the lengths of a side and the altitude on it.AStatement-1 is True, Statement-2 is true, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement- 2 is True.Consider the two similar triangles ABC and DEF. Which of the following is correct about the ratio of the area of the triangle ABCandDEF ?
A(ABDE)=(EFBC)=(ACDF)B(ABDE)2=(BCEF)2=(ACDF)2C(ABDE)=(BCEF)=(DFAC)DNone of theseConsider the two similar triangles ABC and DEF. Which of the following is correct about the ratio of the area of the triangle ABCandDEF ?
A(ABDE)=(EFBC)=(ACDF)B(ABDE)2=(BCEF)2=(ACDF)2C(ABDE)=(BCEF)=(DFAC)DNone of these
A square, a circle and equilateral triangle have same perimeter. Consider the following statements. I. The area of square is greater than the area of the triangle. II. The area of circle is less than the area of triangle. Which of the statement is/are correct?
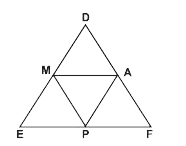
View SolutionM, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
View SolutionTriangle ABC and DEF are similar. If AC = 19 cm and DF = 8 cm , the ratio of the area of two triangles are :
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View SolutionAn equilateral triangle, a square and a circle have equal perimeters. If T denotes the area of triangle, S, the area of square and C, the area of the circle, then :
View Solution
