If triangle ABC is similar to triangle PQR , Perimeter of triangle ABC = 30 cm , Perimeter of triangle = 45 cm , PR = 9 cm then find AC.
To solve the problem, we will use the properties of similar triangles. Since triangle ABC is similar to triangle PQR, the ratios of their corresponding sides are equal to the ratio of their perimeters.
1. Identify the Ratios of the Perimeters:
Ratio of perimeters=Perimeter of ABCPerimeter of PQR=30 cm45 cm=23
Hint: To find the ratio of the perimeters, simply divide the perimeter of triangle ABC by the perimeter of triangle PQR.
2. Set Up the Corresponding Side Ratios:
Since the triangles are similar, we can set up the ratio of the corresponding sides:
ACPR=23
Hint: Remember that for similar triangles, the ratio of any two corresponding sides is the same as the ratio of their perimeters.
3. Substitute the Known Value:
We know that PR=9 cm. Substitute this value into the ratio:
AC9=23
Hint: When substituting, ensure that you maintain the equality of the ratios.
4. Cross-Multiply to Solve for AC:
Cross-multiply to find the value of AC:
3⋅AC=2⋅9
3⋅AC=18
Hint: Cross-multiplication helps eliminate the fraction, making it easier to solve for the unknown variable.
5. Divide to Isolate AC:
Now, divide both sides by 3 to isolate AC:
AC=183=6 cm
Hint: To isolate the variable, perform the opposite operation (in this case, division) on both sides of the equation.
Final Answer:
The length of side AC is 6 cm.
Ratio of perimeters=Perimeter of ABCPerimeter of PQR=30 cm45 cm=23
Since the triangles are similar, we can set up the ratio of the corresponding sides:
ACPR=23
We know that PR=9 cm. Substitute this value into the ratio:
AC9=23
Cross-multiply to find the value of AC:
3⋅AC=2⋅9
3⋅AC=18
Now, divide both sides by 3 to isolate AC:
AC=183=6 cm
The length of side AC is 6 cm.
Topper's Solved these Questions
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
Explore 11 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
Explore 8 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
Explore 5 Videos
- COORDINATE GEOMETRYBook:OSWAL PUBLICATIONChapter:COORDINATE GEOMETRYExercise:SELF ASSESSMENT
Explore 20 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
Similar Questions
If ΔABC~ΔPQR , perimeter of ΔABC=32cm,perimeter of ΔPQR = 48 cm and PR = 6 cm, then find the length of AC.
View Solution△ABC~△RQP and PQ = 10 cm QR = 12 cm and RP = 18 cm. If ar(△ABC):ar(△PQR)=4:9, then AB is equals to :
△ABC~△RQP है तथा PQ = 10 cm QR = 12 cm and RP = 18 cm है | यदि ar(△ABC):ar(△PQR)=4:9, है, तो AB की लंबाई ज्ञात करें |
View Solution
Knowledge Check
If ΔABC ~ ΔPQR, then evaluate the length of AC, if perimeter of ΔABC = 20 cm, perimeter of ΔPQR = 40 cm and PR= 8 cm.
A4 cmB6 cmC10 cmD3 cmThe midpoints of the sides of an equilateral triangle PQR are X, Y and Z. If the perimeter of triangle PQR is 24 cm. then what is the perimeter of triangle XYZ?
A96 cmB36 cmC12 cmD48 cm
△ABC~△QRP and AB = 8 cm , BC = 12 cm and AC = 6 cm. If ar(△ABC):ar(△PQR) = 16: 25, then RQ is equal to:
△ABC~△QRP है और PQ = 6cm, QR = 8cm तथा PR = 10cm है । यदि ar(△ABC):ar(△PQR) = 16:25 है, तो RQ ज्ञात करें |
View Solution△ABC~△PRQ and PQ = 4 cm, QR = 7 cm and PR = 8 cm. If ar(△ABC):ar(△PRQ) = 1 : 4 , then AC is equal to :
△ABC~△PRQ है और PQ =4 cm, QR = 7 cm तथा PR = 8 cm है । यदि ar(△ABC):ar(△PRQ) = 1 : 4 है, तो AC का मान क्या होगा ?
View Solution△ABC~△RQP and AB = 4 cm , BC = 6 cm and AC = 5 cm. If ar(△ABC):ar(△PQR)=9:4, then PQ is equals to :
△ABC~△RQP है तथा AB = 4 सेमी, BC = 6 सेमी और AC = 5 सेमी है | यदि ar(△ABC):ar(△PQR)=9:4,है, तो PQ किसके बराबर है ?
View SolutionIf △ABC~△QPR and △ABC△PQR=94,AC = 12 cm and AB= 18 cm and BC = 15 cm then PR is equal to :
मान लीजिये कि △ABC~△QPR तथा △ABC△PQR=94 हैं AC = 12 सेमी तथा AB= 18 सेमी और BC = 15 सेमी है, तो PR किसके बराबर है ?
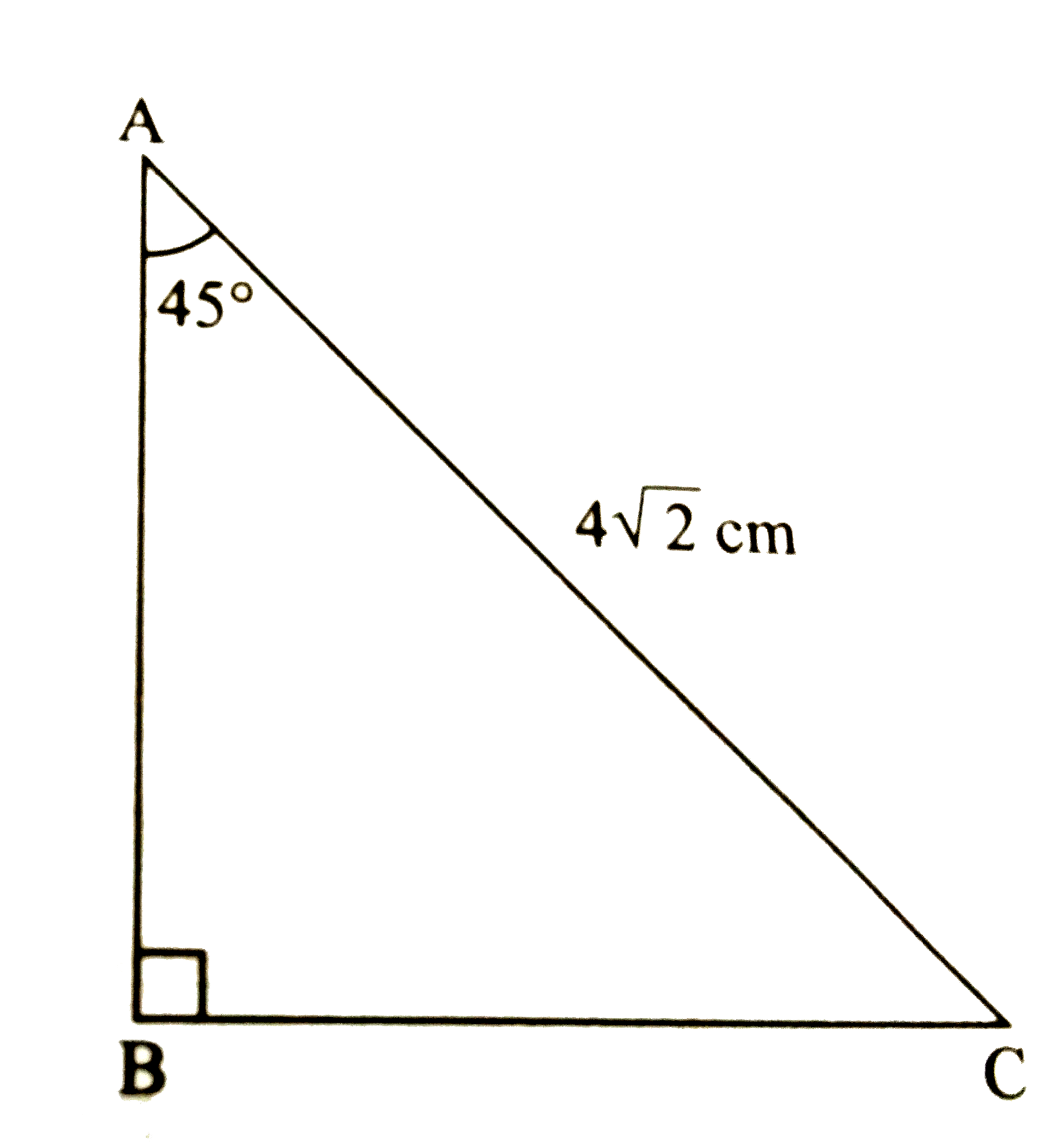
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the difference between perimeter of triangle ABC and perimeter of triangle ADC ?
View Solution
