Find the maximum induced emf.
The correct Answer is:B
To find the maximum induced electromotive force (emf) in a rotating coil placed in a magnetic field, we can follow these steps:
1. Understanding the Setup:
We have a coil placed in a magnetic field that is perpendicular to the plane of the coil. The coil is rotated with an angular velocity ω.
2. Magnetic Flux Calculation:
The magnetic flux Φ through the coil can be expressed as:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the coil's surface. As the coil rotates, θ changes with time, and we can express it as:
θ=ωt
Therefore, the flux becomes:
Φ=B⋅A⋅cos(ωt)
3. Induced EMF Calculation:
According to Faraday's law of electromagnetic induction, the induced emf E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for flux:
E=−ddt(B⋅A⋅cos(ωt))
This simplifies to:
E=B⋅A⋅ω⋅sin(ωt)
4. Finding Maximum Induced EMF:
The maximum value of sin(ωt) is 1. Therefore, the maximum induced emf Emax can be expressed as:
Emax=B⋅A⋅ω
5. Area of the Coil:
If we assume the coil is circular with radius r, the area A is given by:
A=πr2
Substituting this into the equation for maximum induced emf:
Emax=B⋅(πr2)⋅ω
Final Expression:
Thus, the maximum induced emf is:
Emax=B⋅πr2⋅ω
We have a coil placed in a magnetic field that is perpendicular to the plane of the coil. The coil is rotated with an angular velocity ω.
The magnetic flux Φ through the coil can be expressed as:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the coil's surface. As the coil rotates, θ changes with time, and we can express it as:
θ=ωt
Therefore, the flux becomes:
Φ=B⋅A⋅cos(ωt)
According to Faraday's law of electromagnetic induction, the induced emf E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for flux:
E=−ddt(B⋅A⋅cos(ωt))
This simplifies to:
E=B⋅A⋅ω⋅sin(ωt)
The maximum value of sin(ωt) is 1. Therefore, the maximum induced emf Emax can be expressed as:
Emax=B⋅A⋅ω
If we assume the coil is circular with radius r, the area A is given by:
A=πr2
Substituting this into the equation for maximum induced emf:
Emax=B⋅(πr2)⋅ω
Thus, the maximum induced emf is:
Emax=B⋅πr2⋅ω
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
The current through a coil of inductance 5 mH is reversed from 5A to −5A in 0.01 s. What is the maximum self-induced emf in the coil?
View SolutionA closed coil having 50 turns is rotated in a uniform magnetic field B=2×10T about a diameter which is perpendicular to the field.The angular velocity of rotation is 300 revolutions per minute.The area of the coil is 100cm2 and its resistance is 4Ω.Find (a) the averatage emf developed in half a turn from a position where the coil is perpendicular to the magnetic field (b)the average emf in a full turn (c )the net charge flown in part (a) and (d) the emf induced as a function of time if it is zero at t=0 and is increasing in positive direction (e)the maximum emf induced. (f)the average of the squares of emf induced over a long period
View Solution
Knowledge Check
If ϕ=0.02cos100 at weber/turns and number of turns is 50 in the coil , the maximum induced emf is equal to -
A314 voltB100 voltC31.4 voltD6.28 voltA flat, rectangular coil is placed in a uniform magnetic field and rotated about an axis passing through its centre, parallel to its shorter edges and perpendicular to the filed. The maximum emf induced is E. If the axis is shifted to coincide with one of the shorter edges, the maximum induced emf will be
AzeroBE/2CED2EWhich of the following can produce maximum induced emf?
A50 ampere DCB50 ampere 50 Hz ACC50 ampere 500 Hz ACD100 ampere DC
A circular coil of one turn of radiius 5.0 cm is rotated about a diameter with a constatn angular speed of 80 revolutions per minute. A uniform magnetic field B =0.010 T exists in a directon perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c ) the average of the squares of emf induced over a long period.
View SolutionA conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusodially with time as B=B0sinωt where B0=0.20T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ=(τ900)s and (c) the emf induced at t=(π600)s.
View SolutionA square loop of edge a having N turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B exists in the vertical direction. Find
(a) the emf induced ion the coil as a function of time t
(b) the maximum emf induced
(c) the average emf induced in the loop over a long period (d) the average of the squares of emf induced over a long period
(e) if resistance of loop is R , amount of change flow in time t=0 to t=2T
(f) heat produced in time t=0 to =4T
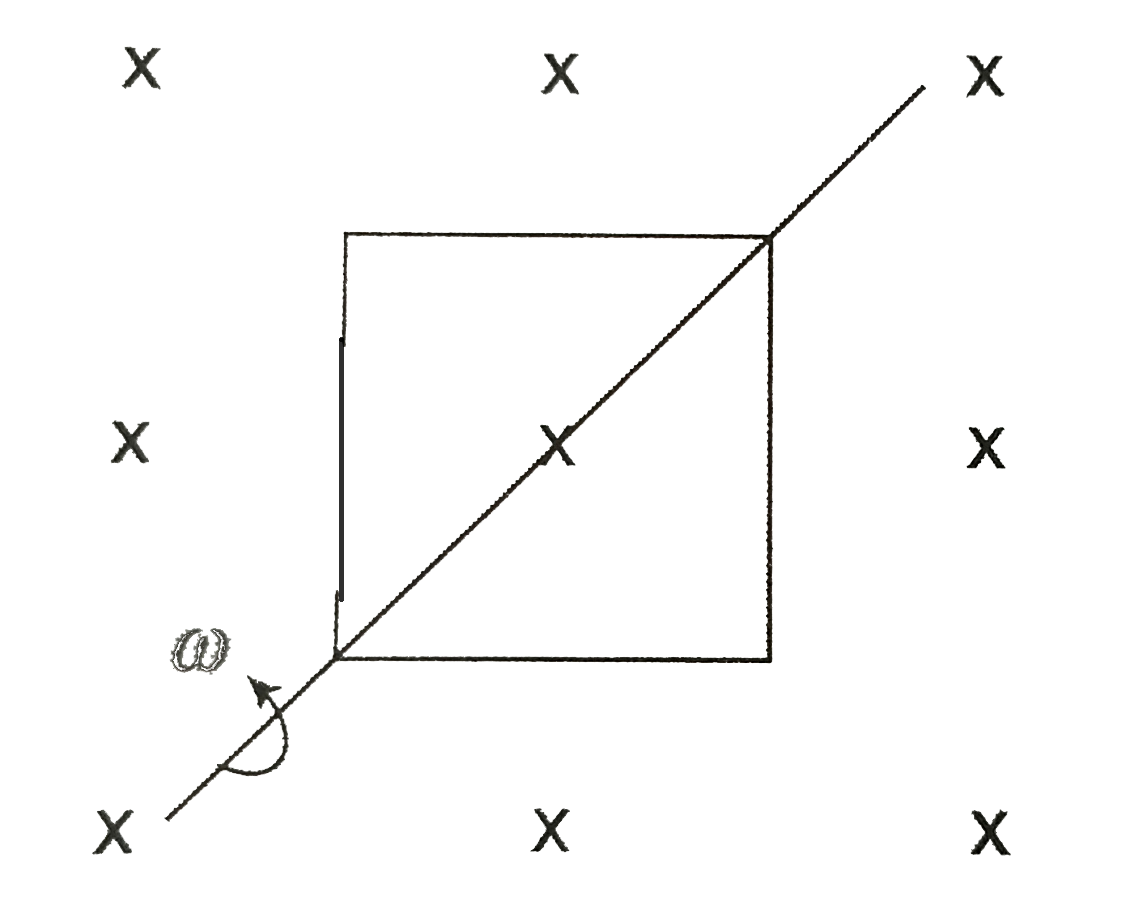
View SolutionA rod PQ of length l is rotating about end P, with an angular velocity ω. Due to electrifugal forceed the free electrons in the rod move toward the end Q and an emf is created. Find the induced emf.

View SolutionFind the emfinduced in the rod in the following cases.The figures are self explanatory.
View Solution
