The electric field between the two spheres of a charged spheres condenser
is zero
is constant
increase with distance from centre
decrease with distance from centre
The correct Answer is:D
Similar Questions
Knowledge Check
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>RThe electric field due to a uniformly charged sphere is maximum at :
Acentre of sphereBinside the surfaceCat the surfaceDat infinite distance from the centreIn the above problem, find the electric field and electric potential at the centre of the sphere due to induced charges on the sphere?
A14π∈0QR2and0B0and14π∈0QRC14π∈0QR2and14π∈0QRD0 and 0
Find the electric field at the center of the sphere due to the induced charges on the surface of the sphere, as shown in Fig. 22-30.

View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
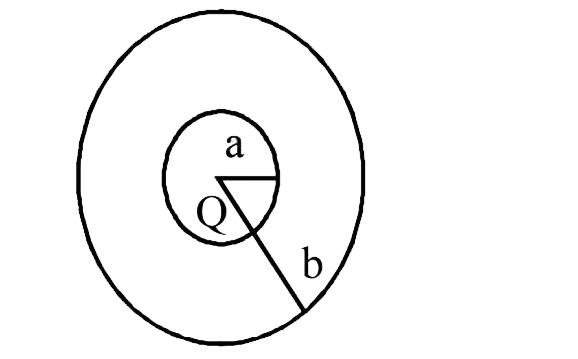
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
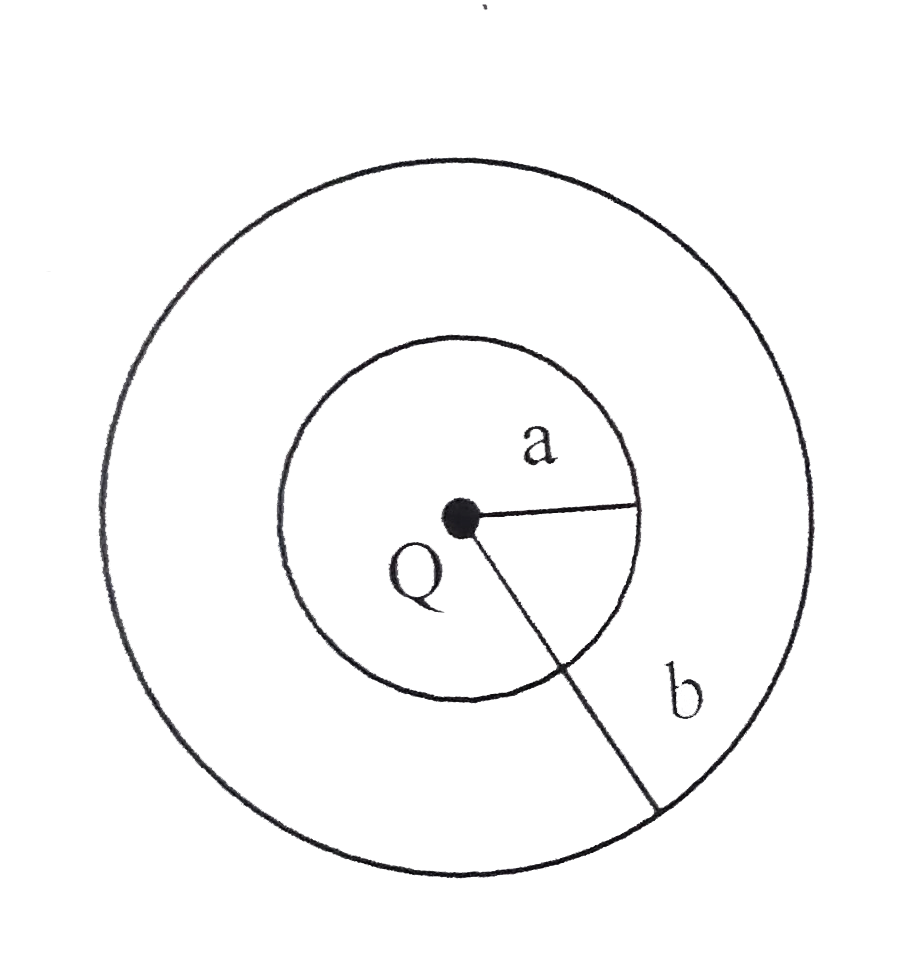
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

View SolutionElectric field intensity due to a charged sphere at a point outside the sphere decreases with ………………...
View Solution
