The electric potential at the centre of a charged conductor is
zero
twice that of the surface
same as on the surface
none of these
The correct Answer is:C
Similar Questions
A spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed outside it. The conductor is initially electrically neutral.
Column I (Cause)Column II (Effect)(A)If outside is shifted to other position(p)Distribution of charge on innner surfaceof cavity charges(B)If inside charge is shifted to other position(q)Distribution of charge on outer surface ofconductor charges(C)If magnitude of charge inside cavity is(r)Electric potential at the centre of conductorincreasedchanges due to charges presenton outer surface of conductor(D)If conductor is earthed(s)Force on the charge placed insidecavity changes
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
Knowledge Check
In the above problem, find the electric field and electric potential at the centre of the sphere due to induced charges on the sphere?
A14π∈0QR2and0B0and14π∈0QRC14π∈0QR2and14π∈0QRD0 and 0Electric potential at the center ofa charged hollow spherical conductor is
AzeroBtwice as that on the surfaceChalf of that on the surfaceDsame as that on the surfaceThe electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπR
A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
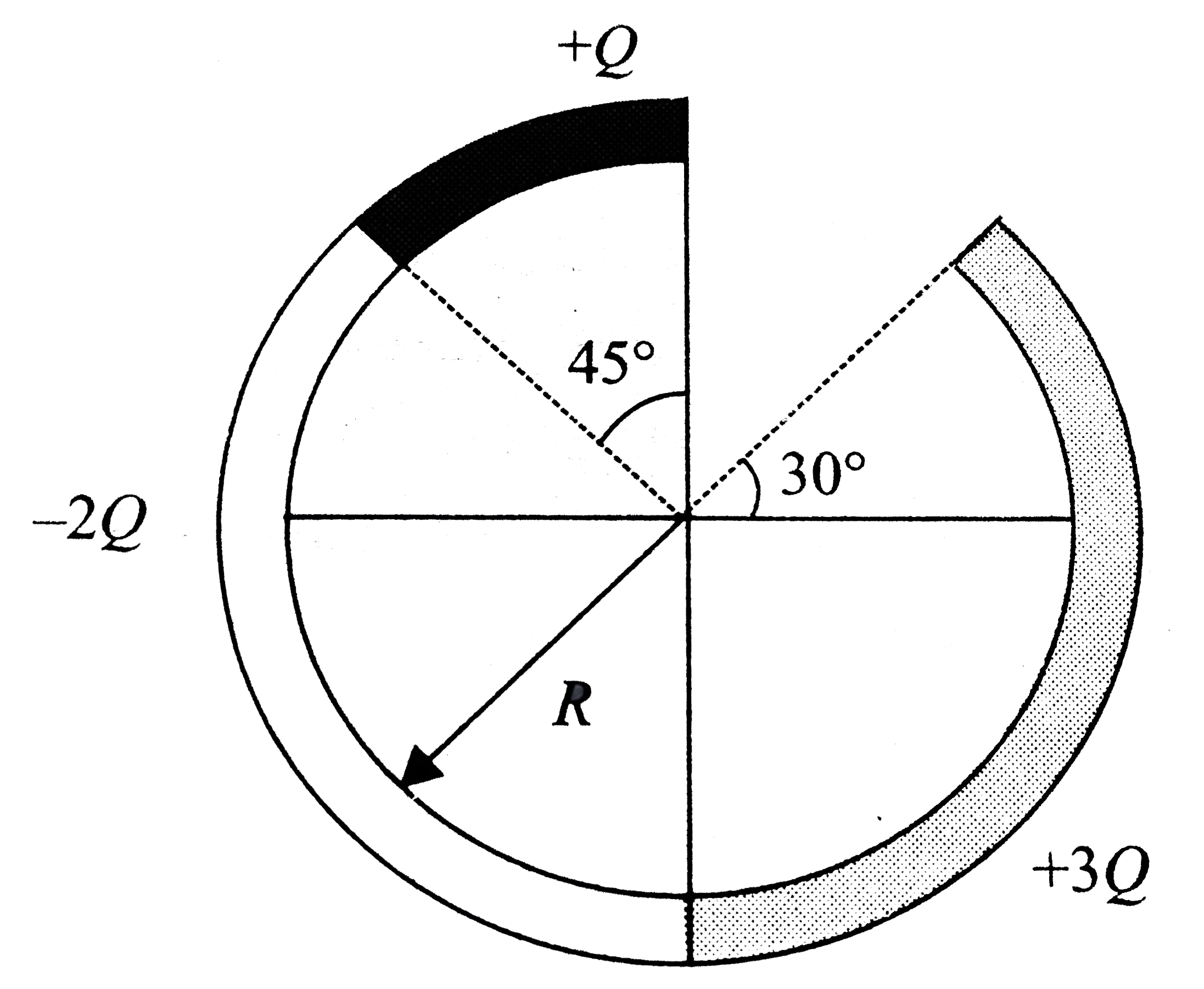 .
.
View SolutionThe electric field at the surface of a charged spherical conductor is 10 KV//m. The electric field at a distance equal to the diameter from its centre will be -
View SolutionThe electric field intensity on the surface of a charged conductor is
View Solution
