A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
zero and Q4πε0R2
Q4πε0R and zero
Q4πε0R and Q4πε0R2
Both are zero
The correct Answer is:B
To solve the problem, we need to determine the electric potential and electric field at the center of a conducting sphere with radius R and charge Q.
1. Understanding the Properties of Conducting Spheres:
- A conducting sphere distributes its charge uniformly on its surface.
- Inside a conducting sphere, the electric field is zero. This is due to the fact that the charges on the surface rearrange themselves in such a way that they cancel any electric field within the conductor.
2. Electric Field at the Center:
- Since the electric field inside a conductor is zero, the electric field at the center of the sphere is:
E=0N/C
3. Electric Potential at the Center:
- The electric potential V inside a conducting sphere is constant and equal to the potential at the surface of the sphere.
- The formula for the electric potential V at the surface of a sphere with charge Q and radius R is given by:
V=Q4πϵ0R
- Since the potential is the same throughout the sphere, the potential at the center is also:
V=Q4πϵ0R
4. Final Results:
- Therefore, the electric potential at the center of the sphere is:
V=Q4πϵ0R
- And the electric field at the center of the sphere is:
E=0N/C
Summary:
- Electric Potential at the center: Q4πϵ0R
- Electric Field at the center: 0N/C
- A conducting sphere distributes its charge uniformly on its surface.
- Inside a conducting sphere, the electric field is zero. This is due to the fact that the charges on the surface rearrange themselves in such a way that they cancel any electric field within the conductor.
- Since the electric field inside a conductor is zero, the electric field at the center of the sphere is:
E=0N/C
- The electric potential V inside a conducting sphere is constant and equal to the potential at the surface of the sphere.
- The formula for the electric potential V at the surface of a sphere with charge Q and radius R is given by:
V=Q4πϵ0R
- Since the potential is the same throughout the sphere, the potential at the center is also:
V=Q4πϵ0R
- Therefore, the electric potential at the center of the sphere is:
V=Q4πϵ0R
- And the electric field at the center of the sphere is:
E=0N/C
- Electric Potential at the center: Q4πϵ0R
- Electric Field at the center: 0N/C
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises17videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
A conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA hollow insulated conducting sphere is given a positive charge of 10μC . What will be the electric field at the centre of the sphere it is radius is 2 metres ?
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is
 View Solution
View SolutionBoth the ring and the conducting sphere are given the same charge Q. Determine the potential of the sphere. Assume that the centre of the sphere lies on the axis of th ring. Is it necessary that the charge on the ring be uniformly distributed to answer the above question ?
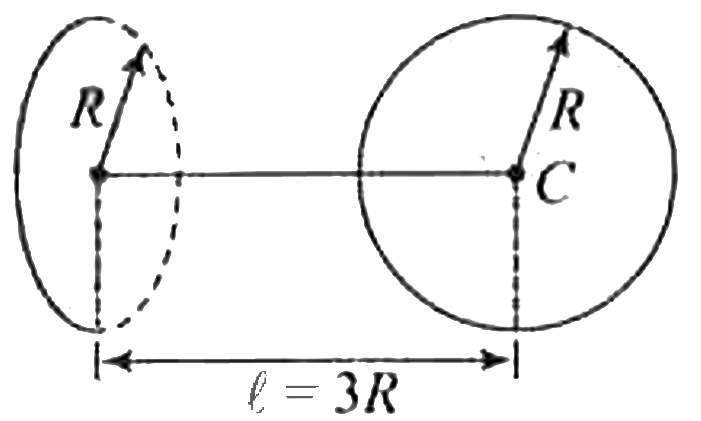 View Solution
View Solutionn charged drops, each of radius r and charge q, coalesce to from a big drop of radius R and charge Q. If V is the electric potential and E is the electric field at the surface of a drop, then.
View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionAt a point 20cm from the centre of a uniformly charged dielectric sphere of radius 10cm, the electric field is 100V/m. The electric field at 3cm from the centre of the sphere will be
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
View Solution

