Question

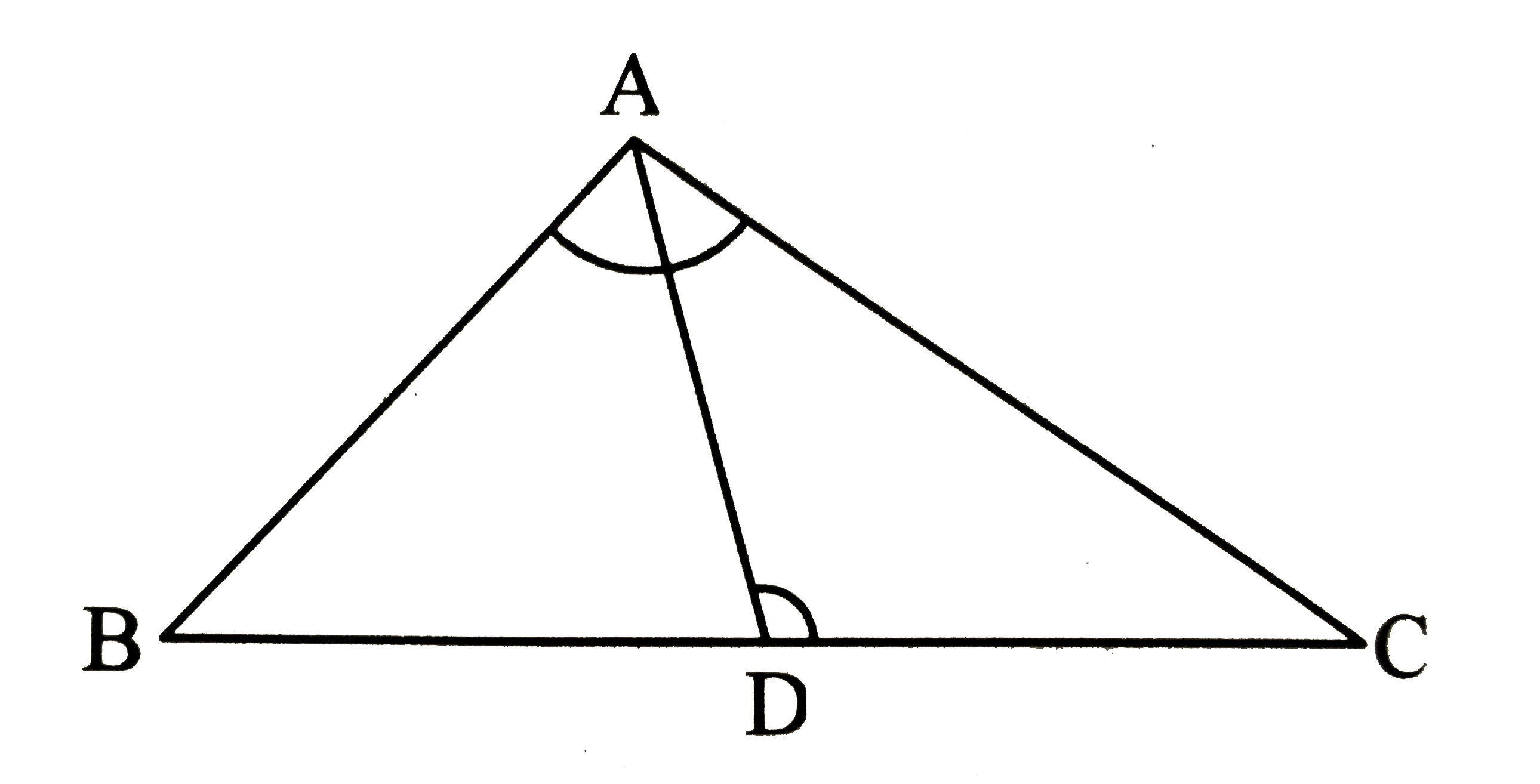
Point D lies on side BC of a ${\displaystyle \Delta ABC}$ such that ${\displaystyle \angle ADC=\angle BAC}$. If ${\displaystyle CB=8cm,BD=6cm}$ then CA is

Options

A. `4sqrt(3)cm`
B. `4cm`
C. `2cm`
D. `16cm`

Answer

B

Explanation

To solve the problem step by step, we will use the properties of similar triangles.

1. Identify the Given Information:
- We have triangle \( \Delta ABC \) with point \( D \) on side \( BC \).
- Given:
- \( CB = 8 \, \text{cm} \)
- \( BD = 6 \, \text{cm} \)
- We need to find \( CA \).

2. Calculate the Length of \( CD \):
- Since \( D \) lies on \( BC \), we can find \( CD \) as follows:
\( CD = CB - BD = 8 \, \text{cm} - 6 \, \text{cm} = 2 \, \text{cm} \)

3. Establish Similar Triangles:
- We know that \( \angle ADC = \angle BAC \) (given).
- Both triangles \( \Delta BAC \) and \( \Delta ADC \) share angle \( C \).
- Therefore, by the Angle-Angle (AA) criterion, we can conclude that:
\( \Delta BAC \sim \Delta ADC \)

4. Set Up the Proportionality of Sides:
- From the similarity of triangles, we have the following proportion:
\( \frac{BC}{AC} = \frac{CD}{AD} \)

5. Substitute the Known Values:
- We know:
- \( BC = 8 \, \text{cm} \)
- \( CD = 2 \, \text{cm} \)
- Let \( AC = x \) and \( AD = x - 2 \) (since \( CD = 2 \, \text{cm} \)).
- Thus, we can write:
\( \frac{8}{x} = \frac{2}{x - 2} \)

6. Cross-Multiply to Solve for \( x \):
- Cross-multiplying gives:
\( 8(x - 2) = 2x \)
- Expanding this:
\( 8x - 16 = 2x \)
- Rearranging:
\( 8x - 2x = 16 \implies 6x = 16 \implies x = \frac{16}{6} = \frac{8}{3} \, \text{cm} \)

7. Final Calculation for \( AC \):
- Therefore, the length of \( CA \) is:
\( AC = \frac{8}{3} \, \text{cm} \approx 2.67 \, \text{cm} \)

Final Answer:
The length of \( CA \) is \( \frac{8}{3} \, \text{cm} \) or approximately \( 2.67 \, \text{cm} \).