Let two lines p and q be parallel. Consider two points B and C on the line p and two points D and E on the line q. The line through Band' E intersects the line through C and D at A in between the two lines p and q. If AC: AD=4:9, then what is the ratio of area of triangle ABC to that of triangle ADE?
2:3
4:9
16:81
1:2
Step by step video & image solution for Let two lines p and q be parallel. Consider two points B and C on the line p and two points D and E on the line q. The line through Band' E intersects the line through C and D at A in between the two lines p and q. If AC: AD=4:9, then what is the ratio of area of triangle ABC to that of triangle ADE? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
Two circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIf lines AB,AC,AD and AE are parallel to a line l show that points A,B,C,D and E are collinear.
View Solution
Knowledge Check
- Question 1 - Select One
If P and Q are two points on the line 3x + 4y = - 15, such that OP = OQ = 9 units, the area of the triangle POQ will be
A18√2 sq unitsB3√2 sq unitsC6√2 sq unitsD15√2 sq units - Question 2 - Select One or More
The point of injtersection of the line xp+yq=1andxq+yp=1 lies on the line
Ax−y=0B(x+y)(p+q)=2qpC(ax+by)(p+q)=(a+b)pqD(ax−by)(p+q)=)a−b)pq
P and Q are two points on the line x−y+1=0. If OP=OQ=6then length of median through O is
View SolutionTwo lines interesect
(A) at a point (B) in a line (C ) at an infinite number of points (D) at two pointsView SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
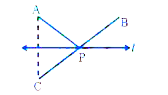
Is the image of P in line l the point P itself ?View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC≅△CDA.
View SolutionTwo different points P and Q are given on one side of line AB. Draw a circle passing through the points P and Q touching the line AB in point R.
View SolutionThe points M and N divide the line seqment AB of ΔABC in three equal parts. If MP||NQ||BC and points P and Q lie on line AC, then prove that P and Q trisect the line AC.
View Solution

