P is a point on the bisector of ∠ABC .If the line through P,parallel to BA meet at Q ,prove that BPO is an isosceles triangle.
Given we have P is a point on the bisector of ∠ABC and draw the line through P parallel to BA and meet BC at Q .
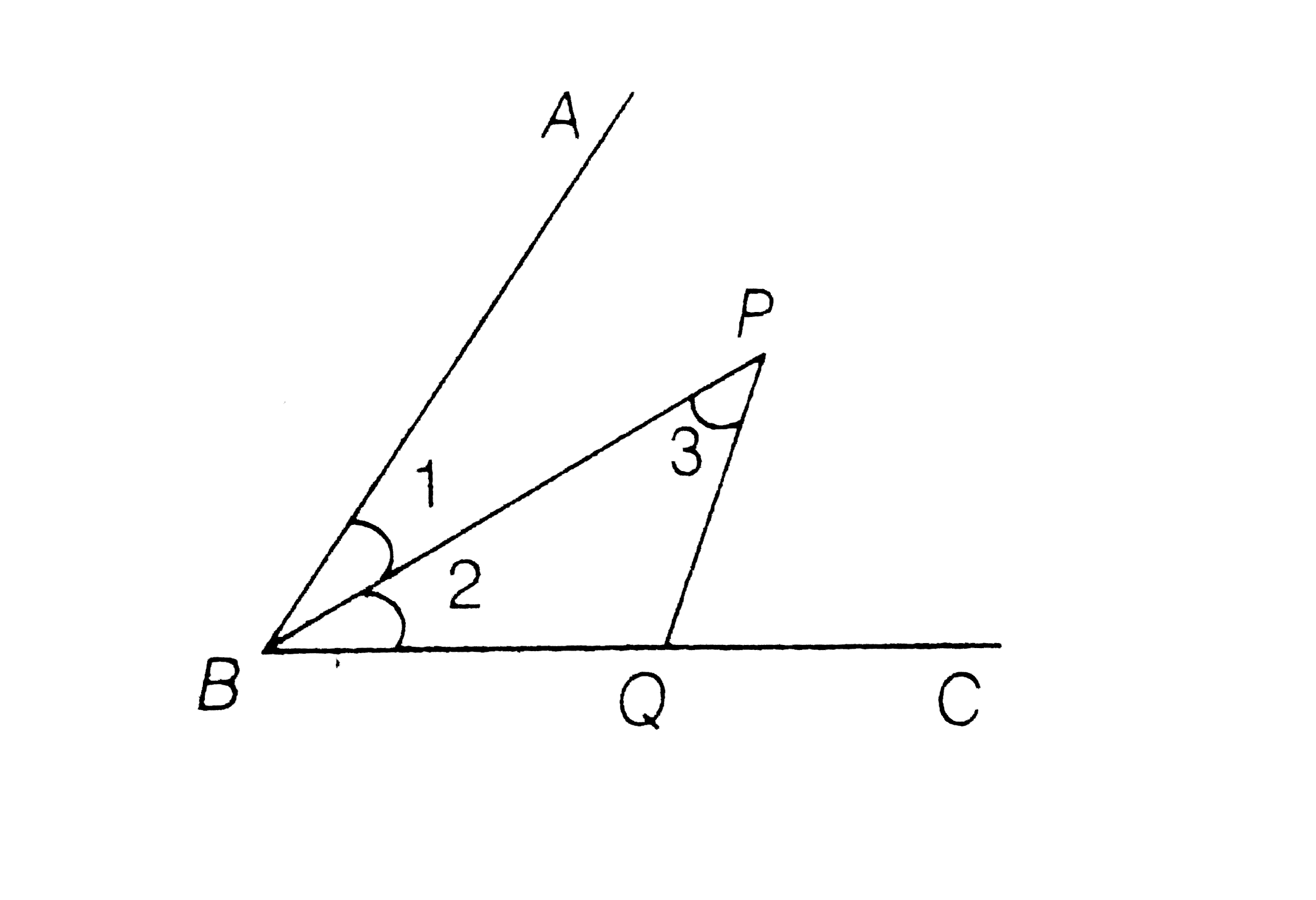
To prove ΔBPQ is an isosceles triangle .
Proof ∠1=∠2 [∵ BP is bisector of ∠B(given )]
Now ∠1=∠3 [alternate interior angles as PQ|| AB ]
thefore ∠2=∠3
⇒ PQ=BQ [sides opposite to equal angles are equal ]
Hence ΔBPQ is an isosceles triangle.
Topper's Solved these Questions
Similar Questions
P is a point on the bisector of an angle ∠ABC. If the line through P parallel to AB meets BC at Q , prove that triangle BPQ is isosceles.
View SolutionThe line 3x+2y=24 meets x - axis at B and the y -axis at A. The perpendicular bisector of AB meets the line through (0, -1) parallel to x -axis at C, then the area of the triangle ABC is_____
View Solution
Knowledge Check
- Question 1 - Select One
ABC is a cyclic triangle and the bisectors of ∠BAC,∠ABCand∠BCA meet the circle at P,Q and R respectively. Then the angle ∠RQP is:
A90∘−∠B2B90∘+∠B2C90∘+∠C2D90∘+∠B2
Pis a point inside the triangle ABC. Lines are drawn through P, parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas 4,9and49sq. units. The area of thetriangle ABC is -
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionIf the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIn the triangle ABC, the base BC is trisected
at D and E. The line through D, parallel to
AB, meets AC at F and the line through E
parallel to AC meets AB at G. Let EG and
DF intersect at H. What is the ratio of the
sum of the area of parallelogram AGHF and
the area of the triangle DHE to the area of
the triangle ABC ?View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionLet P be an interior point of a triangle ABC whose side lengths are 26, 65, 78. The line through P parallel to BC meets AB in K and AC in L. The line through P parallel to CA mmets BC in M and BA ln N. The line through P parallel to AB meets CA ln S and CB ln T. If KL, MN, ST are of equal lengths, find this common length.
View Solution

