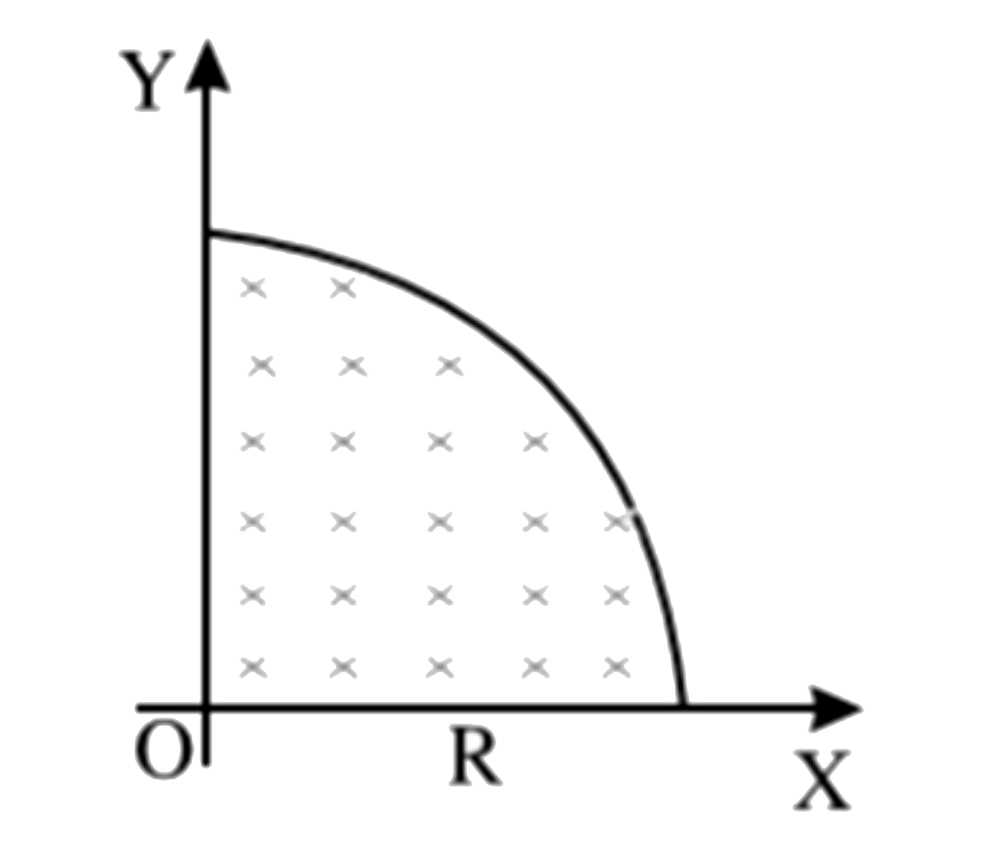
R त्रिज्या की चौथाई डिस्क में (चित्र देखिये) एकसमान पृष्ठ आवेश घनत्व σ है। बिंदु (O,O, Z) पर विद्युत विभव को ज्ञात कीजिये।
σ8ε0[1−Z√R2+Z2]
σ4ε0[√R2+Z2+Z]
σ8ε0[√R2+Z2−Z]
σ8ε0[1+Z√R2+Z2]
The correct Answer is:C
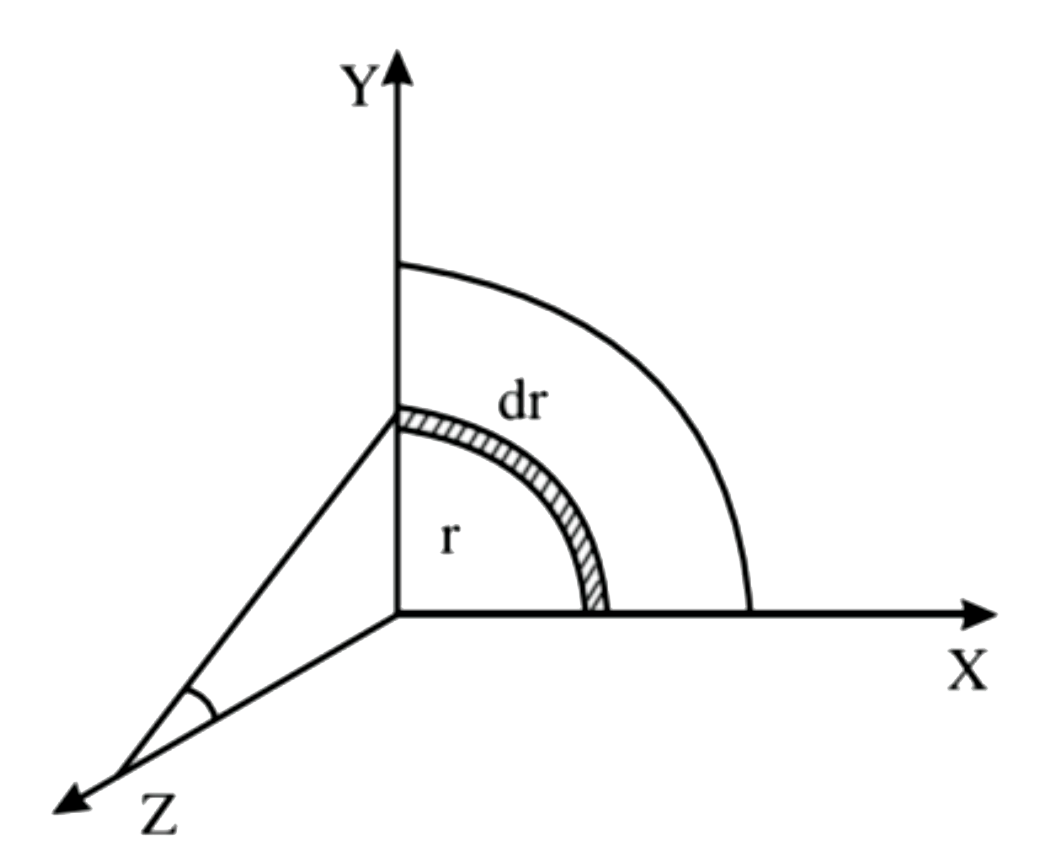
V=∫R0kαπrdrα√r2+z2=σ8ε0∫R0rdr√r2+z2
t2=r2+z2
tdt=rdr
V=σ8ε0∫√22+R2zdt
=σ8ε0(√R2+z2−z)
Topper's Solved these Questions
Similar Questions
v चाल से गतिमान एक H- परमाणु विराम अवस्था में एक अन्य H - परमाणु के साथ सम्मुख प्रत्यक्ष संघट्ट करता है। दोनों परमाणु मूल अवस्था में हैं। वेग v का न्यूनतम मान जिसके लिए कम से कम एक परमाणु उत्तेजित हो सकता है, है
04:52View Solutionनिकाय का प्रारंभिक विन्यास चित्र में दिखाया गया है।
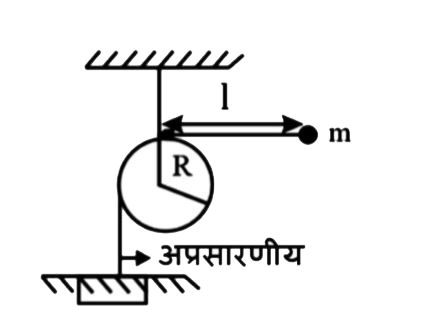
डोरी और घिरनी हल्की हैं। गोलक को मुक्त किया जाता है और डोरी घिरनी के चारों ओर लिपटना शुरू कर देती है। (घिरनी केंद्र पर अनुप्रयुक्त बल द्वारा स्थान पर रखी जाती है)
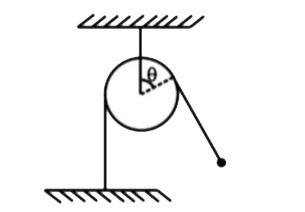
वह दर r ज्ञात कीजिए जिससे घिरनी के चारों ओर लपेटी गई डोरी की लंबाई बढ़ती ( θ के फलन के रूप में) है।03:55View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
01:36View Solutionबिन्दुओ (4,-1,2) और (-3,2,3) को मिलाने वाली रेखा एक समतल को बिंदु (-10,5,4) पर लंबवत मिलती है समतल का समीकरण ज्ञात कीजिये
44:40View Solutionबिंदु (3,4,0) की XY तल से लामिबक दुरी ज्ञात कीजिये
41:34View Solutionस्थिरवैद्युत विभव | बिंदु आवेश के कारण विभव | आवेशों के निकाय के कारण विभव
55:18View Solutionआवेश की परिभाषा | आवेश के प्रकार | इलेक्ट्रॉनों की बहाव | विद्युत धारा | विद्युत परिपथ | विद्युत विभव | विद्युत विभवांतर
50:12View Solutionबिन्दु-आवेशों के समूह के कारण विद्युत विभव || समविभव पृष्ठ, || विभव प्रवणता : विभव-प्रवणता तथा विद्युत क्षेत्र की तीव्रता में सम्बन्ध,
49:59View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
36:26View Solutionविद्युत क्षेत्र एवं विधुत विभव में सम्बन्ध|समविभव पृष्ठ
01:23:57View Solutionआवेश घनत्व | विद्युत क्षेत्र
02:01View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
43:13View SolutionIn a circle centred at O, AB is a chord and C is any point on AB such that OC is perpendicular to AB. If the radius of the circle is 10 cm and OC = 6 cm, then the length of the chord is: एक वृत्त में O केंद्र है , AB एक जीवा है और C, AB पर कोई बिंदु है जैसे OC, AB पर लंबवत है। यदि वृत्त की त्रिज्या 10 सेमी और OC = 6 सेमी है, तो जीवा की लंबाई ज्ञात करे |
01:16:44View Solutionविधुत विभव क्या होता है #!#बिंदु आवेश के लिए विभव का सूत्र
01:18:14View SolutionRevision|विद्युत द्विध्रुव के कारण सामान्य बिंदु पर विद्युत क्षेत्र|विद्युत द्विध्रुव के कारण विद्युत विभव|समरूप विद्युत क्षेत्र में विद्युत द्विध्रुव|चालक|OMR|Summary
01:17:43View Solutionप्रश्न|विद्युत विभव|विभव से सम्बंधित मुख्य बिंदु|विद्युत क्षेत्र में दो बिन्दुओ के मध्य विभवांतर|बिंदु आवेश के कारण विद्युत विभव|वैद्युत द्विध्रुव|वैद्युत द्विध्रुव आघूर्ण|वैद्युत द्विध्रुव के कारण विद्युत क्षेत्र|OMR|Summary
48:20View Solution

