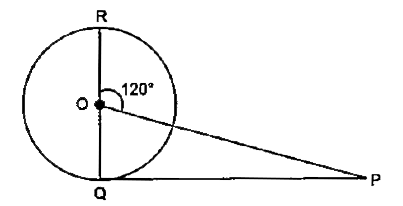
The tangents drawn at the point P and Q of a circle centered at O meet at A. If ∠POQ=120∘, then what is the ratio of ∠PAQ:∠PAO?
2:3
4:1
2:1
5:2
The correct Answer is:C
To solve the problem, we need to find the ratio of angles ∠PAQ to ∠PAO given that ∠POQ=120∘.
1. Draw the Circle and Points:
- Draw a circle with center O.
- Mark points P and Q on the circumference of the circle.
- Draw tangents at points P and Q that meet at point A.
2. Identify Given Angles:
- We know that ∠POQ=120∘.
3. Determine Angles at Point O:
- Since OP and OQ are radii of the circle, the angles ∠OAP and ∠OAQ are both 90∘ because the radius is perpendicular to the tangent at the point of tangency.
4. Calculate Remaining Angle:
- The angles around point O must sum to 360∘. Therefore, we can find ∠AOP and ∠AOQ:
- Since ∠POQ=120∘, the remaining angle ∠AOP+∠AOQ=360∘−120∘=240∘.
- Since ∠AOP and ∠AOQ are equal (as OP and OQ are equal), we can denote each as x:
2x=240∘⟹x=120∘
Thus, ∠AOP=∠AOQ=120∘.
5. Find Angle PAQ:
- Now, we can find ∠PAQ:
∠PAQ=∠POQ−∠AOP=120∘−120∘=0∘
However, this is incorrect as we should consider the angles formed by the tangents.
- The angle ∠PAQ is actually half of ∠POQ because of the properties of tangents:
∠PAQ=12×∠POQ=12×120∘=60∘
6. Find Angle PAO:
- Since ∠PAO=90∘ (as established earlier), we now have:
∠PAO=90∘
7. Calculate the Ratio:
- Now we can find the ratio of ∠PAQ to ∠PAO:
Ratio=∠PAQ∠PAO=60∘90∘=23
Final Answer:
The ratio of ∠PAQ:∠PAO=2:3.
- Draw a circle with center O.
- Mark points P and Q on the circumference of the circle.
- Draw tangents at points P and Q that meet at point A.
- We know that ∠POQ=120∘.
- Since OP and OQ are radii of the circle, the angles ∠OAP and ∠OAQ are both 90∘ because the radius is perpendicular to the tangent at the point of tangency.
- The angles around point O must sum to 360∘. Therefore, we can find ∠AOP and ∠AOQ:
- Since ∠POQ=120∘, the remaining angle ∠AOP+∠AOQ=360∘−120∘=240∘.
- Since ∠AOP and ∠AOQ are equal (as OP and OQ are equal), we can denote each as x:
2x=240∘⟹x=120∘
Thus, ∠AOP=∠AOQ=120∘.
- Now, we can find ∠PAQ:
∠PAQ=∠POQ−∠AOP=120∘−120∘=0∘
However, this is incorrect as we should consider the angles formed by the tangents.
- The angle ∠PAQ is actually half of ∠POQ because of the properties of tangents:
∠PAQ=12×∠POQ=12×120∘=60∘
- Since ∠PAO=90∘ (as established earlier), we now have:
∠PAO=90∘
- Now we can find the ratio of ∠PAQ to ∠PAO:
Ratio=∠PAQ∠PAO=60∘90∘=23
The ratio of ∠PAQ:∠PAO=2:3.
Similar Questions
The centre of the circle is O. Two tangents are drawn from the point of the circle A & B, which meets at the point P. Accordingly if ∠AOB=120∘, then find out the ratio of ∠APB:∠AOP?
View SolutionPQ is a tangent drawn from an external point P to a circle with center O, ∠QOR is the diameter of the circle. If ∠POR=120∘. What is the measure of ∠OPQ?
View Solution
Knowledge Check
Two tangents drawn at the points A and B of a circle centred at O meet at P. If ∠AOB=120∘ then ∠APB:∠APO is
A2:3B4:1C2:1D5:2Two tangents drawn at the points A and B of a circle centred at O meet at P. If ∠AOB=120∘ then ∠APB:∠APO is
A2:5B3:2C4:1D2:1The tangents drawn at point A and B of a circle with centre O, meet at P. If ∠AOB=120∘ and AP = 6 cm, then what is the area of triangle APB (in cm2) ?
A6√3B8√3C9D9√3
There is only _______ tangent drawn at a point on the circle.
View SolutionThe tangents drawn at points A and B of a circle with centre O, meet at P. If ∠AOB=120∘ and AP=6cm then what is the area of quad APB (in cm2) ?
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
View SolutionO is the centre of the circle and two tangents are drawn from a point P to this circle at points A and B. If ∠AOP=50∘, then what is the value (in degrees) of ∠APB?
View SolutionTwo tangents are drawn from a point P to a circle at Q and R. If O is the centre of the circle and ∠QOP=40∘, then what is the value (in degrees) of ∠QPR?
View Solution
