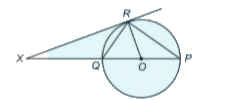
Two tangents are drawn from a point P to a circle at Q and R. If O is the centre of the circle and ∠QOP=40∘, then what is the value (in degrees) of ∠QPR?
60
80
90
100
The correct Answer is:D
To solve the problem, we need to find the value of angle QPR given that two tangents are drawn from point P to a circle at points Q and R, and the angle QOP is 40 degrees.
1. Understanding the Geometry:
- Let O be the center of the circle.
- Points Q and R are the points where the tangents touch the circle.
- The angles formed by the radius and the tangent at the point of contact are right angles. Therefore, angle OQP and angle ORP are both 90 degrees.
2. Identifying Angles:
- We know that angle QOP = 40 degrees.
- Since the tangents from a point outside the circle are equal, angle QOP = angle ROP = 40 degrees.
3. Finding Angle AOP:
- The angle AOP (where A is the point P) can be calculated as follows:
Angle AOB=Angle QOP+Angle ROP=40∘+40∘=80∘
4. Using the Exterior Angle Theorem:
- The angle QPR is an exterior angle for triangle OQP, which can be expressed as:
Angle QPR=Angle OQP+Angle OQP
- Since angle OQP = 90 degrees, we can substitute:
Angle QPR=90∘−Angle QOP
- Therefore, we have:
Angle QPR=90∘−40∘=50∘
5. Final Calculation:
- Thus, the value of angle QPR is:
Angle QPR=100∘
Conclusion:
The value of angle QPR is 100 degrees.
- Let O be the center of the circle.
- Points Q and R are the points where the tangents touch the circle.
- The angles formed by the radius and the tangent at the point of contact are right angles. Therefore, angle OQP and angle ORP are both 90 degrees.
- We know that angle QOP = 40 degrees.
- Since the tangents from a point outside the circle are equal, angle QOP = angle ROP = 40 degrees.
- The angle AOP (where A is the point P) can be calculated as follows:
Angle AOB=Angle QOP+Angle ROP=40∘+40∘=80∘
- The angle QPR is an exterior angle for triangle OQP, which can be expressed as:
Angle QPR=Angle OQP+Angle OQP
- Since angle OQP = 90 degrees, we can substitute:
Angle QPR=90∘−Angle QOP
- Therefore, we have:
Angle QPR=90∘−40∘=50∘
- Thus, the value of angle QPR is:
Angle QPR=100∘
The value of angle QPR is 100 degrees.
Similar Questions
Knowledge Check
Two tangents are drawn from a point P to a circle at Q and R. If O is the centre of the circle and ∠QOP=40∘, then what is the value (in degrees) of ∠QPR?
A60B80C90D100Two tangents are drawn from a point P to a circle at A and B. O is the centre of the circle. If ∠AOP=60∘, then ∠APB is
A120∘B90∘C60∘D30∘O is the centre of the circle and two tangents are drawn from a point P to this circle at points A and B. If ∠AOP=50∘, then what is the value (in degrees) of ∠APB?
A60B80C90D100
Two tangents AB and AC are drawn from an external point A to a circle with centre O . If they are inclined to each other at an angle of 100∘ then what is the value of ∠BOC.
View SolutionXR is a tangent to the circle. O is the centre of the circle. If ∠XRP=120∘, then what is the value (in degrees) of ∠QOR?
View SolutionIn the given figure. 0 is centre of the circle. Circle has 3 tangents. If QPR = 45∘, then what is the value (in degrees) of ∠QOR?

View SolutionIn figure PR is tangent to the circle at P and O is the centre of the circle. The value of ∠POQ is

View SolutionPQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
View Solution