Question

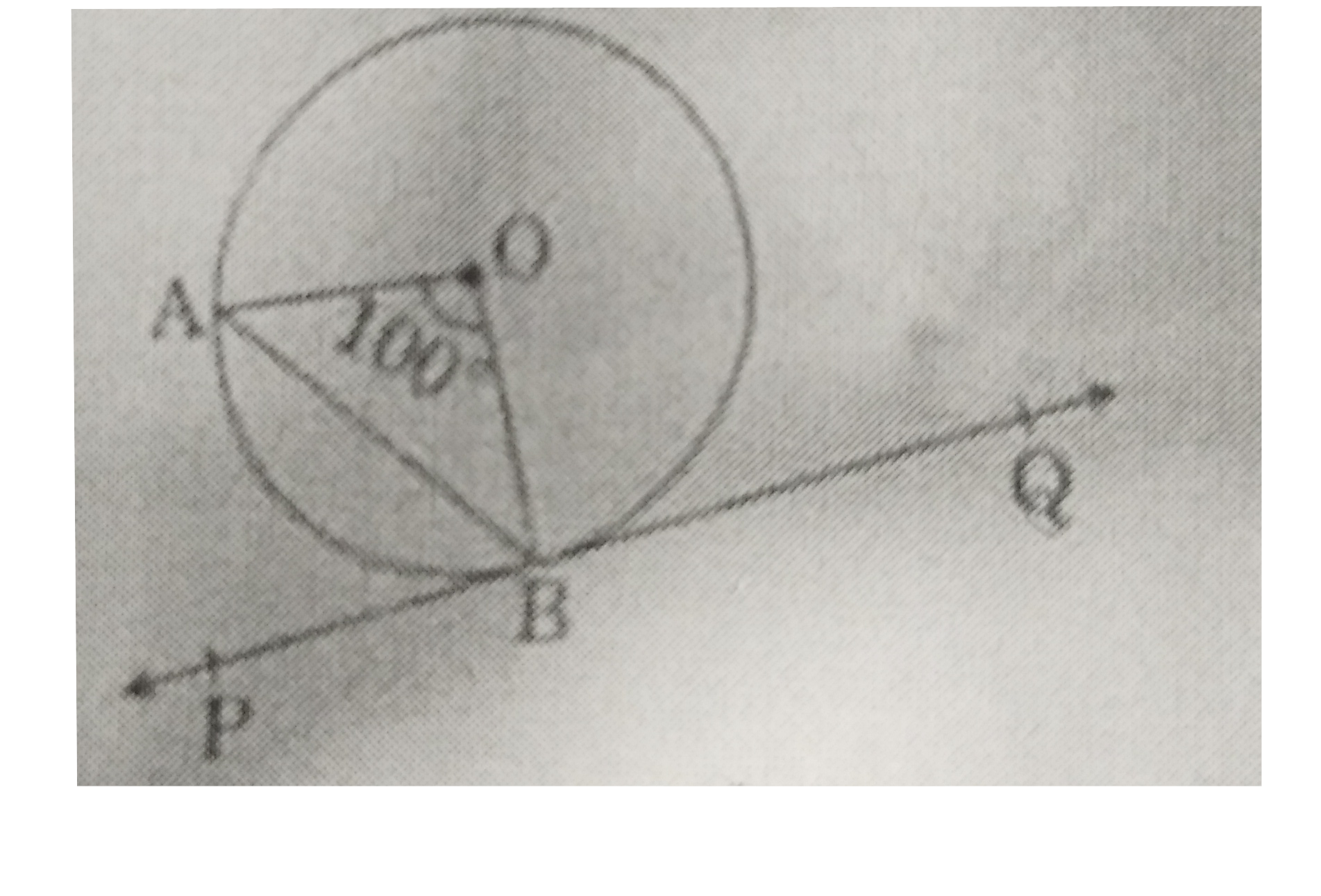
The centre of the circle is O. Two tangents are drawn from the point of the circle A & B, which meets at the point P. Accordingly if $\angle AOB={120}^{\circ }$, then find out the ratio of $\angle APB:\angle AOP$?

Options

A. `2:5`
B. `3:2`
C. `4:1`
D. `2:1`

Explanation

To solve the problem, we need to find the ratio of angles $$\angle APB$$ to $$\angle AOP$$ given that $$\angle AOB={120}^{\circ }$$.

1. Identify the Given Information:
- The center of the circle is \( O \).
- Points \( A \) and \( B \) are points on the circle from which tangents are drawn to point \( P \).
- The angle \( \angle AOB \) is given as \( 120^\circ \).

2. Find \( \angle APB \):
- The angles \( \angle APB \) and \( \angle AOB \) are related because \( AP \) and \( BP \) are tangents to the circle from point \( P \).
- By the property of tangents, we know that \( \angle APB = 180^\circ - \angle AOB \).
- Therefore, \( \angle APB = 180^\circ - 120^\circ = 60^\circ \).

3. Find \( \angle AOP \):
- The angle \( \angle AOP \) is formed by the radius \( OA \) and the tangent \( AP \).
- By the property of tangents, \( \angle AOP = 90^\circ \) since the radius at the point of tangency is perpendicular to the tangent.

4. Calculate the Ratio \( \angle APB : \angle AOP \):
- Now we have:
- \( \angle APB = 60^\circ \)
- \( \angle AOP = 90^\circ \)
- The ratio \( \angle APB : \angle AOP = 60 : 90 \).
- Simplifying this ratio gives \( 2 : 3 \).

Final Answer:
The ratio of \( \angle APB : \angle AOP \) is \( 2 : 3 \).