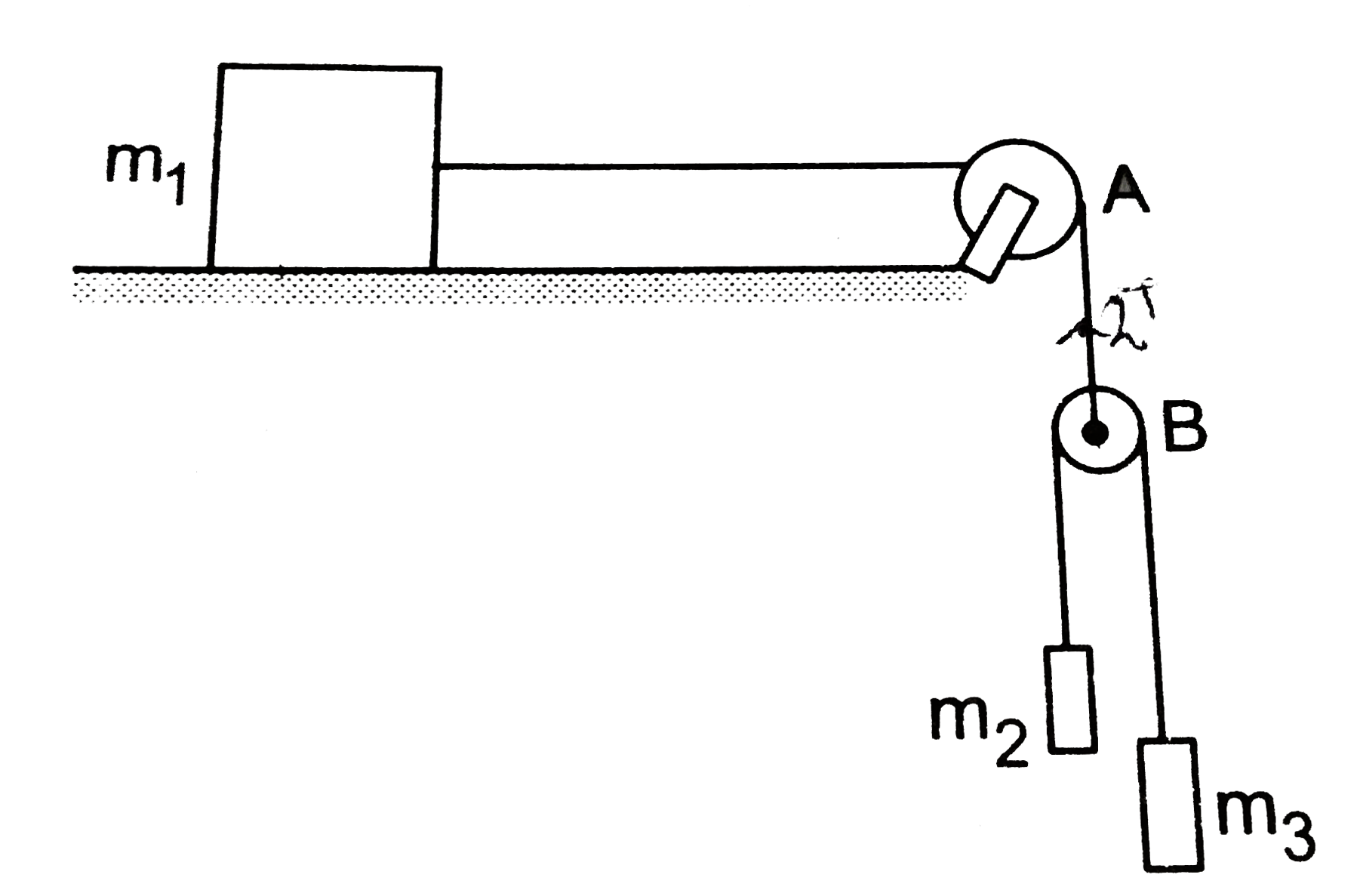
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
 Solution in Tamil
Solution in Tamil
Suppose the acceleration of nq1 is a0 towards right. That will also be the downward acceleration of the pulley B because the string connecting m1andm3 has a constant length. This implies tht the decrease i the separation between m2and B equals the increase in teh separation between m3andB. So, the upward acceleeration of m2 wiht respect to B equals the downward acceleration of m3 with respect of B. Let this acceleration be a
The acceleration of m2 with respect to the ground =a0−a (downward) and the acceleration of m3 with respect to the ground =a0+a (downward).
These accelerations will be used in Newton's laws. Let the tension be T in the upper string and T' in the lower string. consider the motion of the pulley B.

The forces on this light pulley are ltbr> a. T upward by the upper sting and
2T' downwards by thelower string.
As the mass of the pulley is negligible,
2T'−T=0
giving T≡T2............i
Motion m1
THe acceleration is a0 in the horizontal direction. The forces on m1 are
a. T by the string (horizontal)
b. m1 g by theearth (verticlaly downwards) and
N by the table (verrtically upwards).
IN the horizontal direction the equation
T=m1a0
Motion of m2: acceleration is a0−a in the fownward direction. Teh forces on m2 are
a. m2g downward by teh earth and
T'=T2 upward by teh string.
Thus, m2g−T2=m2(a0+a)...........iii
Moton of m3= The aceeleration is (a0+a) downward. The forces on m3 are
a. m3g downward by the earth and
b. T'=T/2 upward by the string. thus,
m3g−T2=m3(a0+0)...........iv.
We want to calculate a0 so we shall elimiN/Ate T and a from ii, iii, and iv.
Putting T from ii in and iii and iv,
a0−a=m2−mI1a02m2=g−m1a02m2
and a0+a+m3g−m−1a02M3=g−m1a02m3
Adding 2a0=2g−m1a02(1m2+1m3)
a0=g−m1a04(1m2+1m3)
or, a0[1+m14(1m−2+1m3)]=g
or,a0=g1+m14(1m2+1m3)
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -114videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises42videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer14videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises34videos
PHYSICS AND MATHEMATICS
Similar Questions
If the tension in the cable supporting an elevator is equal to the weight of the elevator, the elevator may be
04:11View SolutionA block of 2 kg is suspended from the ceiling through a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
07:31View SolutionA block of mass 2 kg placed on a long frictionless horizontal table is pulled horizontally by a constant foerce F. It is found to move 10 m in the first two seconds. Find the magnitude of F.
02:14View SolutionShould the internal energy of a system necessarily increase if heat is added to it?
03:25View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
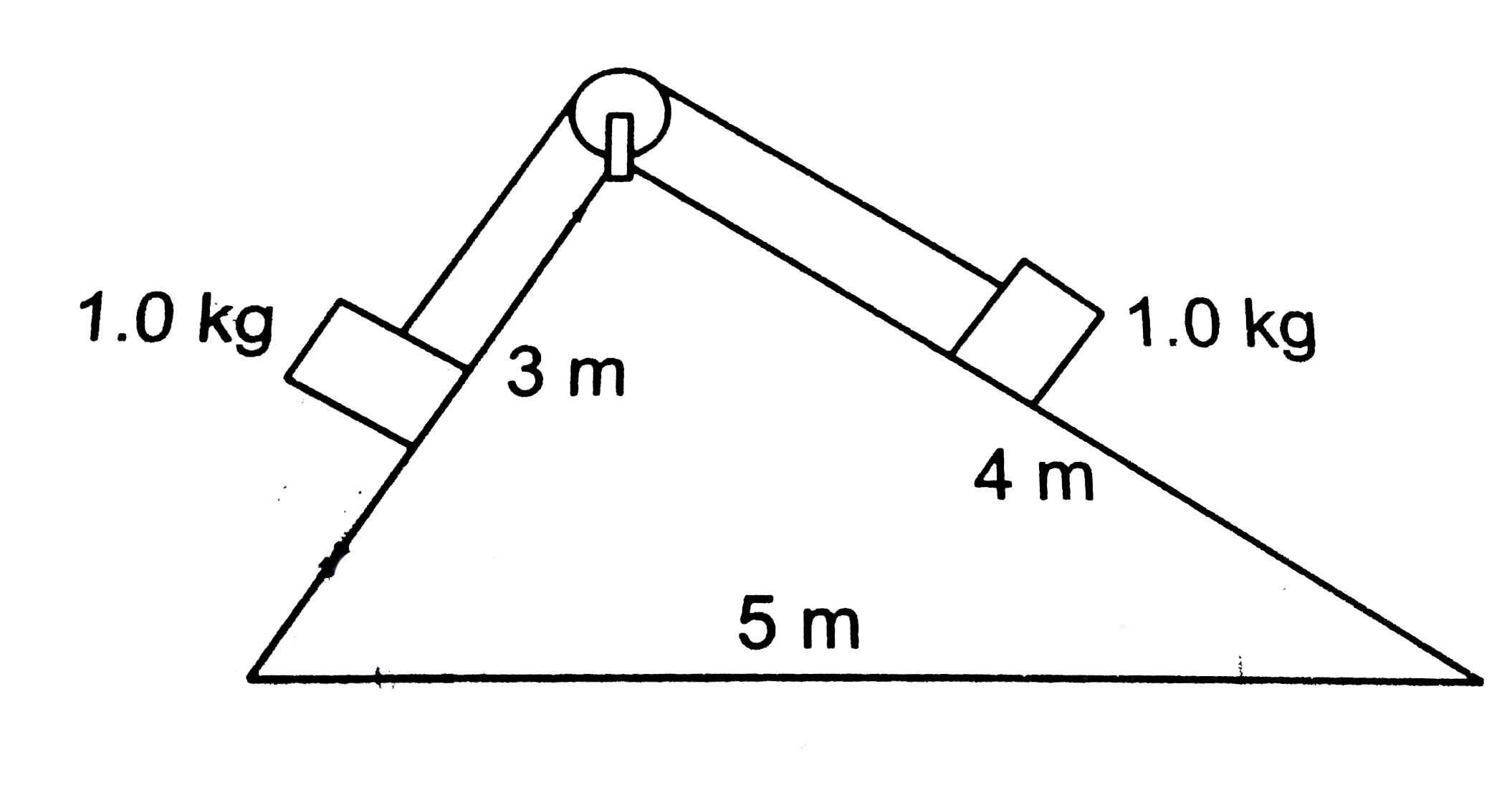
04:25View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
 03:42View Solution
03:42View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 04:23View Solution
04:23View SolutionIf two masses m_1 and m_2 (m_1 gt m_2) tied to string moving over a frictionless pulley, then acceleration of masses
05:16View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.

If a1a2anda3 are the accelerations of masses m1,m2andm3 respectively, then05:09View SolutionIn the arrangement shown in the figure all surfaces are frictionless, the masses of the block are m1=20kgandm2=30kg. The accelerations of masses m1andm2 will be if F = 180N.
 02:31View Solution
02:31View Solutionm1,m2 व m3 द्रव्यमान के तीन पिण्ड क्रमागत द्रव्यमान रहित डोरी से जुड़े हैं और एक घर्षण रहित मेज पर रखे हैं | यदि m3 द्रव्यमान को बल F से खींचा जाए, तो m2 व m3 द्रव्यमानों के बीच डोरी में तनाव होगा :
07:50View Solutionm1,m2 व m3 द्रव्यमान के तीन ब्लॉक प्रदर्शित चित्र में घर्षणहीन मेज पर द्रव्यमानहीन डोरियों द्वारा जुड़े हैं। इन्हें 40 N के बल द्वारा खींचा जाता है। यदि m1= 10kg , m2=6 kg तथा m3=4 kg है। तब तनाव T2 होगा
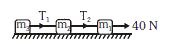 05:09View Solution
05:09View Solutionतीन द्रव्यमान M1,M2 व M3 एक घर्षणरहित मेज पर स्थित है। द्रव्यमान चित्रानुसार द्रव्यमानहीन डोरी से जुड़े हैं। द्रव्यमान M3 को चित्रानुसार नियत बल F द्वारा खींचा जाता है तो द्रव्यमान M2 व M3 के मध्य डोरी में तनाव होगा-
 04:12View Solution
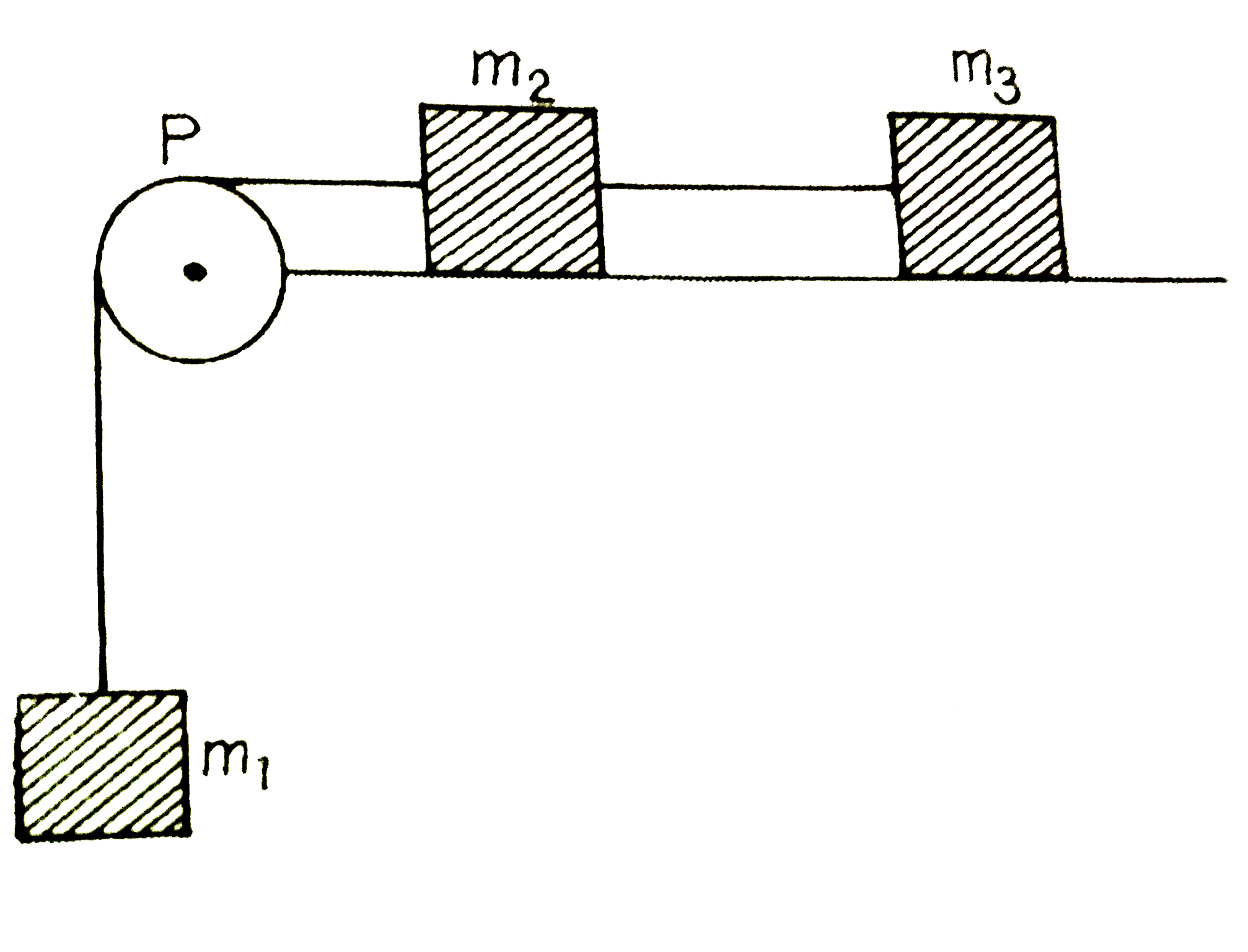
04:12View Solutionयहाँ दर्शाये गये निकाय में तीन पिंड m1,m2 और m3 एक रस्सी से जुड़े है जो एक घिरनी के ऊपर से होकर गुजरती है। m1 मुक्त रूप से लटका है औरm2 तथा m3 एक रुक्ष क्षैतिज मेज पर है, जिसका घर्षण गुणांक =μ है। घिरनी घर्षणरहित है और इसका द्रव्यमान नगण्य है। यदि m1=m2=m3=m है, तो m1 का अधोमुखी (नीचे की ओर) त्वरण होगा:
 05:09View Solution
05:09View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 02:03View Solution
02:03View SolutionTwo unequal masses m1 and m2 are connected by a string which passes over a frictionless and massless pulley. Find the tension in the string and the acceleration of the masses.
04:31View Solution

