Find the mass M of the hanging block in figure which will prevent the smaller block from sliping over the triangular blcok. All the surfaces are frictions and the strings and the pulleys are light.
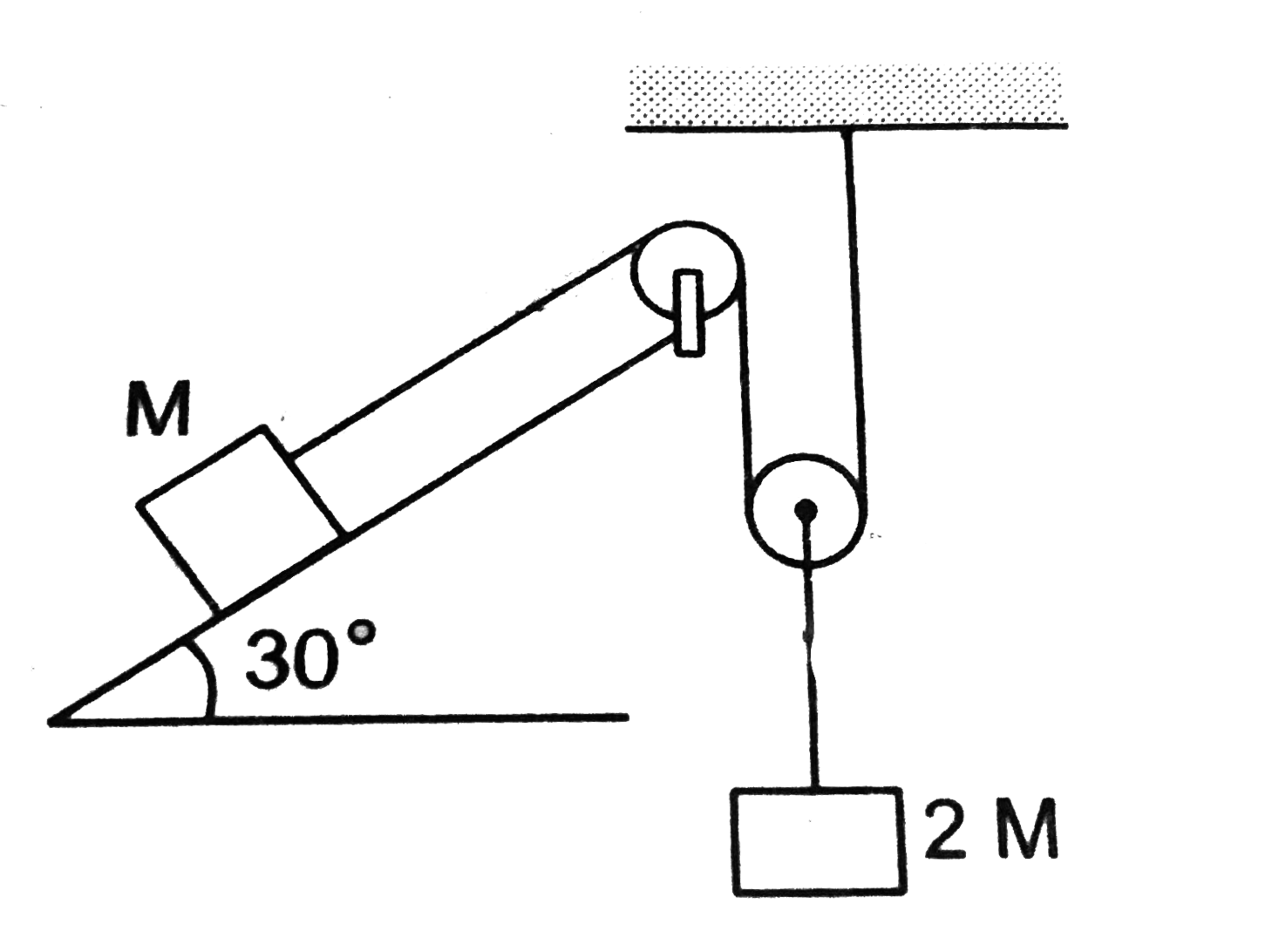 Solution in Tamil
Solution in Tamil

2Ma+mgsinθ−T=0
→T=2Ma+Mgsinθ ….i.
Now2T+2Ma−2Mg=0
From equation i. <br>2(2Ma+Mg sin theta)+2Ma-2Mg=0<br> rarr 4Ma +2Mg sin theta + 2Ma- 2Mg = 0<br> rarr 6Ma + 2Mg sin 30^0 +2Mg=0<br> 6Ma=Mg<br>rarr as= g/6<br>Henceae≤rationofmas,<br> M=2a=2xx g/6 <br> =g/3 up the plane.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
8 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
A refrence frame attached to the earth
View SolutionShould the internal energy of a system necessarily increase if heat is added to it?
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionIn figure m_(1)= 1 kg and m_(2)= 4 kg Find the mass m of the hanging block which will provent the smaller block from slipping over the triangular block .All the surface are frictionless and the string and the pulleys are light
View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.

View Solution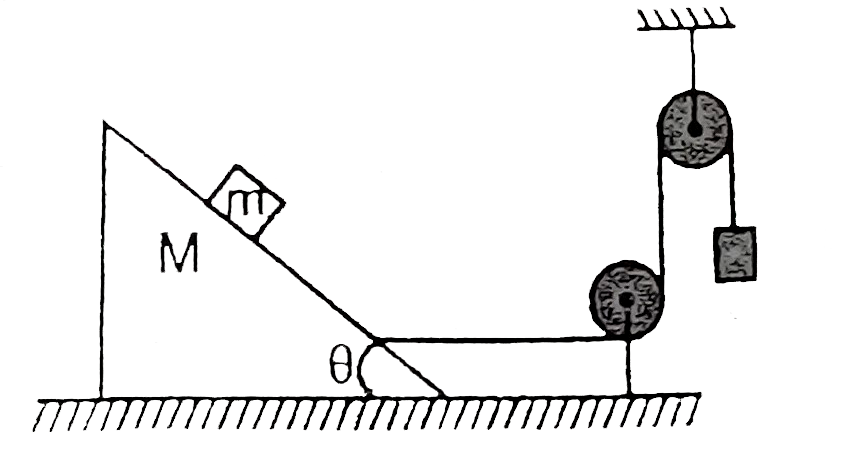
Find the mass (in kg) of the hanging block which will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light. Given m=M=1kg,cotθ=2,
View SolutionFind the mass of the hanging block in which will prevent the smaller block of mass m from slipping over the triangular block of mass M. All the surfaces are frictionless and the strings and the pulleys are light

View SolutionA hanging block of mass m' prevents the smaller block of mass m from slipping over a movable triangular block of mass M. All the surface are frictionless and the strings and the pulleys are light. Value of mass m' in terms of m, M and theta is
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
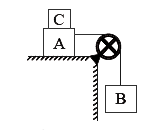
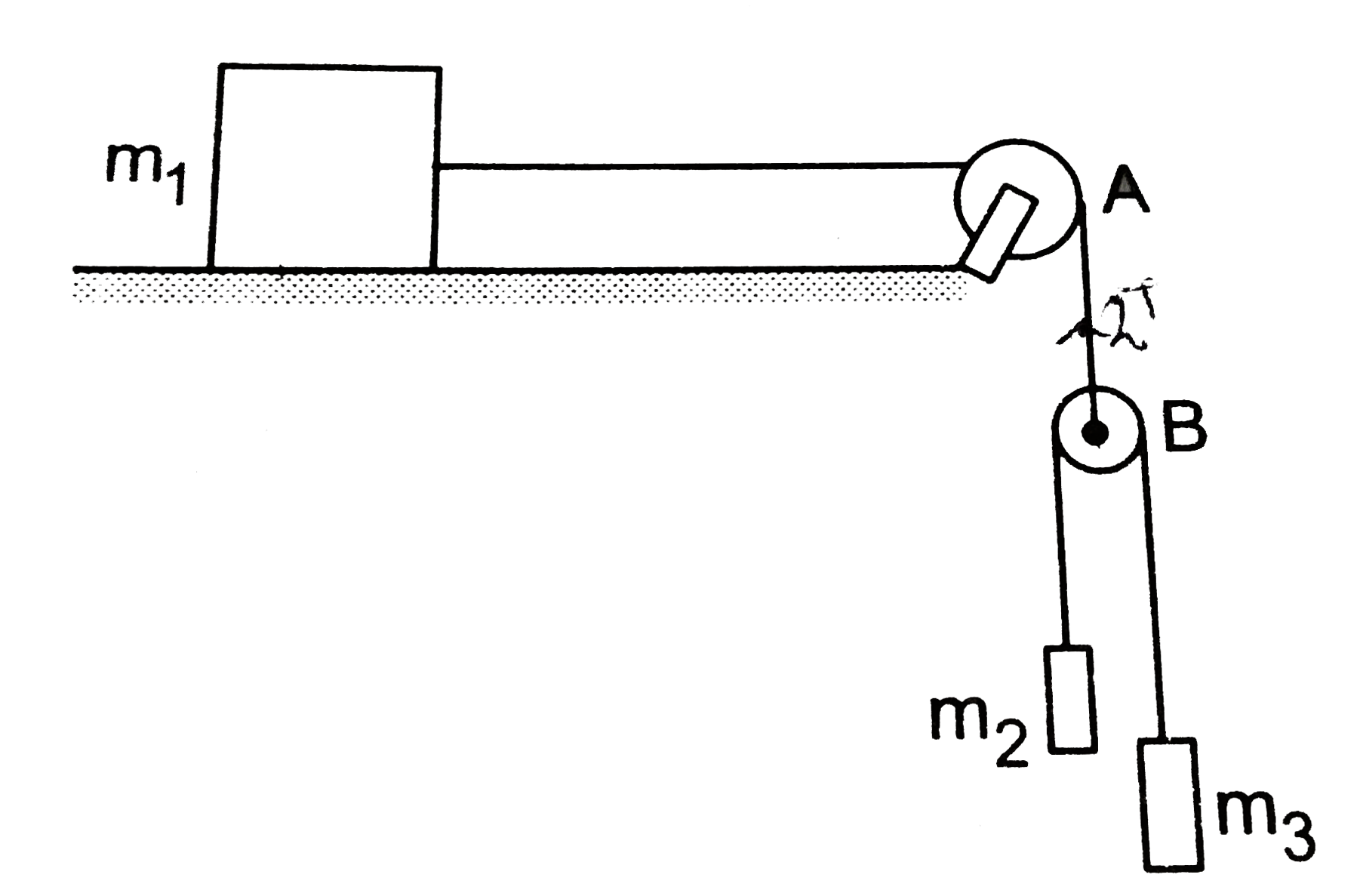
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionIn figure m1=1kg and m2=4kg Find the mass m of the hanging block which will prevent the smaller block from slipping over the triangular block .All the surface are frictionless and the string and the pulleys are light

View SolutionA hanging block of m 'mass prevents a small block of mass m from sliding over a moving triangular block of mass m. All surfaces are frictionless and the cords and pulleys are light. m, M and theta What is the value of mass m 'in terms of?
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution