A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
 Solution in Tamil
Solution in Tamil
Let us take the two blocks plus the spring as the system. The centre of mass of the system moves with an acceleration a=Fm+M. Let us work from a reference frame with its origin at the centre of mass. As this frame is accelerated with respect to the ground we have to apply pseudo force ma towards dlet on tbe block of mass m an Ma towards left on theblock of mass M. The net exterN/Al force on m is
F1=ma=mFm+M towrds left
and the net exterN/Al force on M is
F2=F−Ma=F−MFm+M=mFm+M towards right.
The situation from this frame ils shown in ure. As the centre of mass is at rest in this frame, the blcoks move in opposite directions and come to instantaneous rest at some instant. The extension of the spring will be maximum at this instasnt. Suppose the left block through a distance x2 from the initial positions.
The total work done by the exterN/Al forces F1andF2 in this period are
W=F1x1+F2x2=mFm+M(x1+x2)
This should be equal to the increase in the potential energy of the spring as there is no change in the kinetic energy. Thus,
mFm+M(x1+x2)=12k(x1+x2)2
or, x1+x2=2mFk(m+M)
This is the maximum extension of the spring.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer25videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -118videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises18videos
CALORIMETRY
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises30videos
CIRCULAR MOTION
Similar Questions
Can the centre of mass of a body be at a point outside the body?
04:28View SolutionConsider the following two equations
(A).→R=1M∑imi→ri
and(B).→aCM=→FM
IN a noninertial frame07:36View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
06:53View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
02:49View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
02:16View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
03:52View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
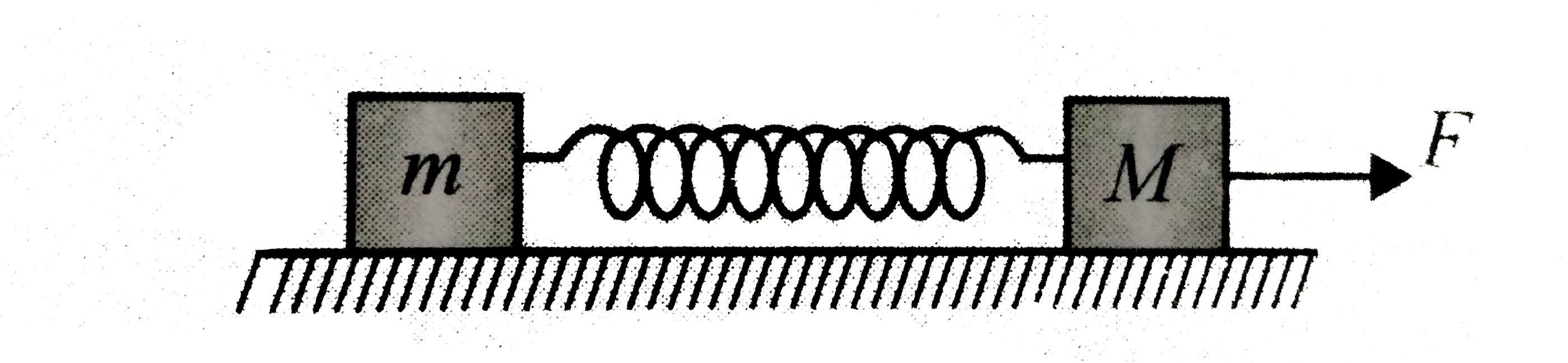 05:57View Solution
05:57View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
03:28View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
04:18View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant K. Blocks are kept on a smooth horizontal plane. Initally both the blocks the at rest and spring is unstressed. Force F is applied on M to right as shownin the figure then which of the following is correct ?
 02:59View Solution
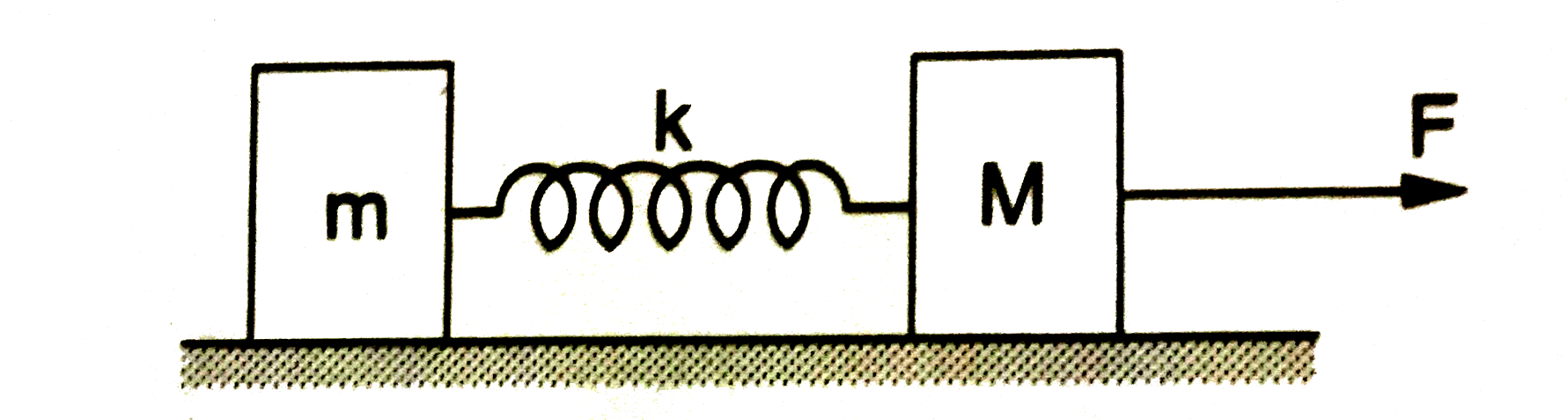
02:59View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
 View Solution
View Solutionm द्रव्यमान का एक ब्लॉक, M द्रव्यमान के दूसरे ब्लॉक से एक द्रव्यमान रहित तथा स्प्रिंग नियतांक K की स्प्रिंग से बँधा है | ब्लॉक चिकने क्षैतिज तल पर रखे हैं | प्रारम्भ में ब्लॉक विरामावस्था में है तथा स्प्रिंग बिना खिंची है | अब यदि M द्रव्यमान के ब्लॉक को एक नियत बल f लगाकर खींचा जाता है तो m द्रव्यमान के ब्लॉक पर लगा बल होगा :
07:27View Solutionद्रव्यमान के एक ब्लॉक को द्रव्यमान M के दूसरे ब्लॉक में स्प्रिंग नियतांक की स्प्रिंग ( द्रव्यमान नगण्य ) द्वारा जोड़ दिया जाता है । ब्लॉक एक चिकने समतल पर रखे हुए हैं । प्रारंभ में ब्लॉक स्थिर है तथा स्प्रिंग सामान्य स्थिति में है, तब द्रव्यमान M के ब्लॉक को एक नियत बल f द्वारा खींचा जाता है । द्रव्यमान m के ब्लॉक पर आरोपित बल होगा -
04:32View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
05:01View Solution

