The descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m^2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.
 Solution in Tamil
Solution in Tamil
The correct Answer is:A, B
A is light pulley and B is the descending puley having I=0.20 kg-m^2 and r=0.2 m
Mass of the block =1kg
According to the question
T1=m1a……….1
(T2−T1)r=Iα……2
m2g=m2αa2=T1+T2……. 3
T2−T1=Ia2r2=5a2
and T1=a (because α=a2r)
→T2=2a

→m2g=m2a2+75a+a
[using 3]
→2Ir2g=2Ir2a2+92as(12mr2=I)
→98.5a+4.5a
→a=989.5=10.3ms2
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -215videos
ROTATIONAL MECHANICS
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises58videos
SIMPLE HARMONIC MOTION
Similar Questions
The axis of rotation of a purely rotating body
07:31View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
04:37View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
05:16View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 02:51View Solution
02:51View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mas 2.0 kg as shown in figure. Find the acceleration of the block.
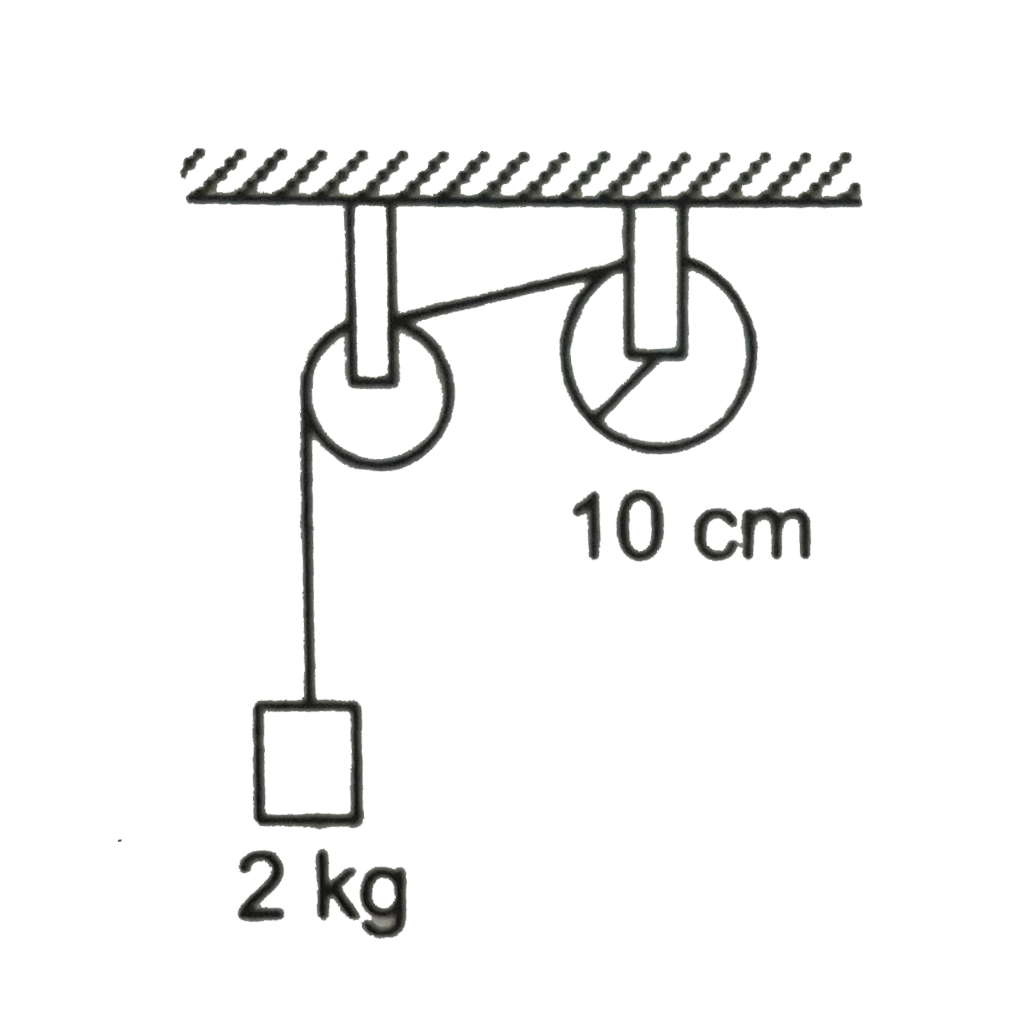 01:34View Solution
01:34View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
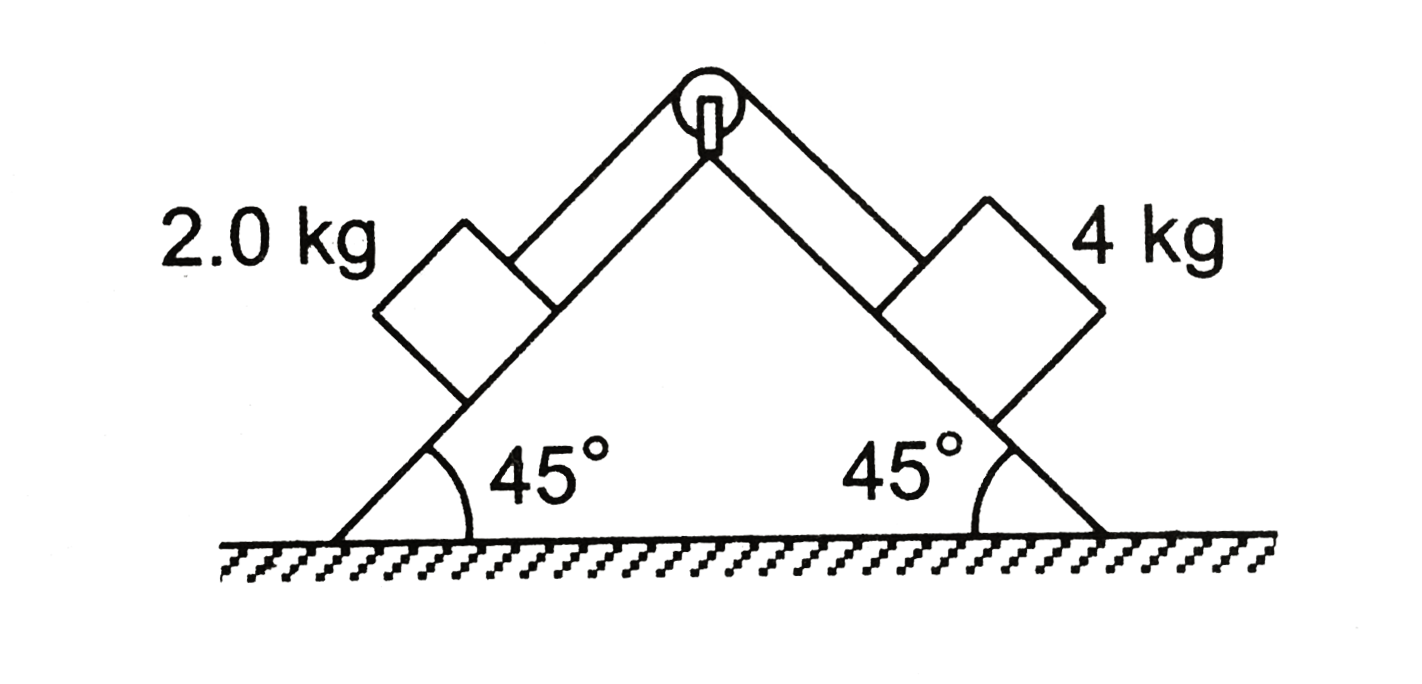 02:39View Solution
02:39View SolutionA small pulley of radius 20 cm and moment of inertia 0.32kg-m^(2) is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition acceleration of the block will be
05:51View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
10:45View SolutionThe blocks A and B are arranged as shown in the figure. The pulley is frictionless. The mass of A is 10 kg . The coefficient of friction of A with the horizontal surface is 0.20. The minimum mass of B to start the motion will be
 04:46View Solution
04:46View SolutionFor the given figure the acceleration of 1 kg block if string is massless and mass of pulley is 2 kg and diameter of pulley is 0.2 m :-
03:35View Solutionचित्र 18.E7 में प्रदर्शित घिरनी की त्रिज्या 10 cm तथा अपने अक्ष के प्रति जड़त्व आघूर्ण 0.5kgm2 है। दोनों नत तल घर्षणरहित हैं। 4.0 kg द्रव्यमान वाल गुटक के त्वरण की गणना करें
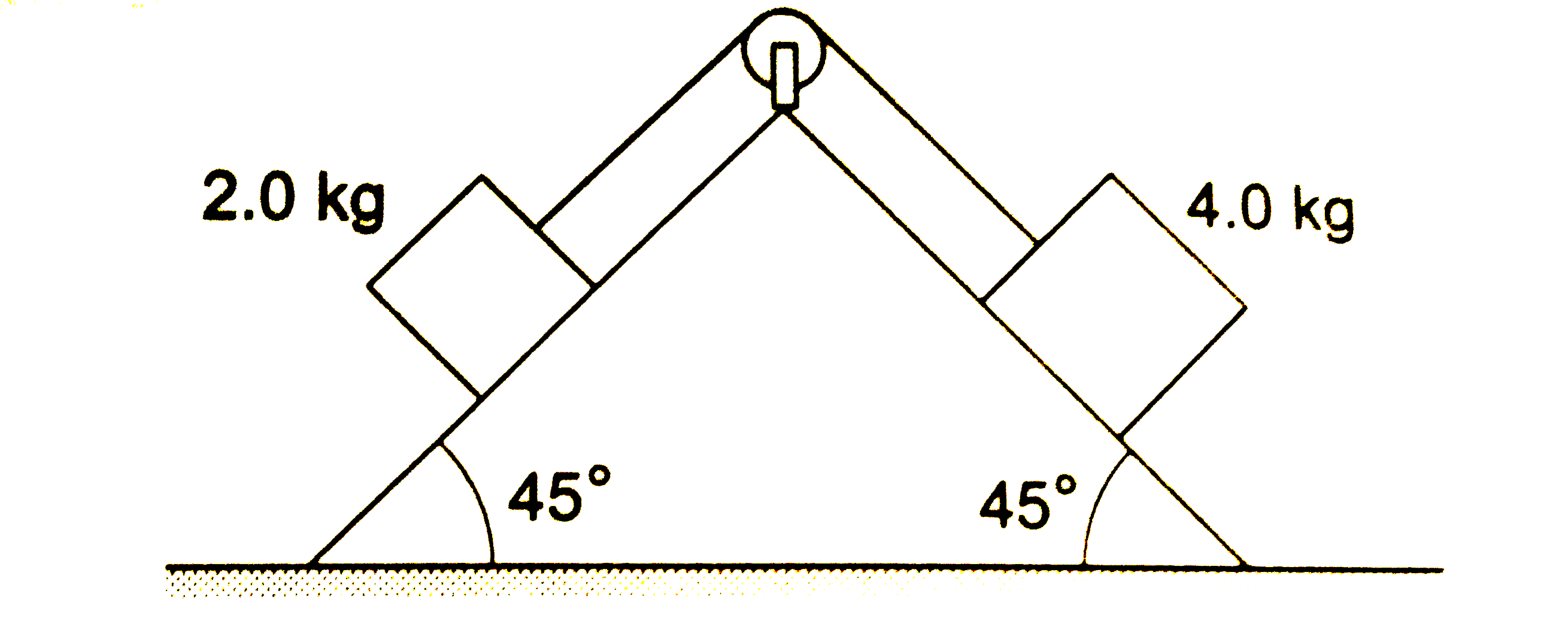 02:31View Solution
02:31View Solutionचित्र में प्रदर्शित नीचे की ओर जा रही घिरनी की त्रिज्या 20 cm तथा अपने अक्ष के प्रति जड़त्व आघूर्ण 0.20kg.m2 है। टेबुल से जुडी स्थिर घिरनी के तथा टेबुल के घर्षण को अनदेखा करे। गुटके का द्रव्यमान 1.0 kg है। गुटके का त्वरण ज्ञात करे।
 05:18View Solution
05:18View SolutionA block of mass 5 kg lies on a horizontal frictionless plane. A string attached to it passes over a smooth pulley fixed to the edge of the plane and carries a load of mass 1 kg. Find the acceleration of the system.
06:41View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 01:36View Solution
01:36View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.
 03:23View Solution
03:23View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
 07:15View Solution
07:15View Solution

