Protons having kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field so that it just misses a plane target kept at a distance I in front of the accelerator. Find the magnetic field.
Redius =1KE=K
since l=μqB
⇒l=√2kmqB
B = (sqrt 2Km ) /(ql)
Topper's Solved these Questions
Similar Questions
If a proton, deuteron, and alpha particle on being accelerated by the same potential difference enters perpendicular to the magnetic field, then the ratio of their kinetic energies is
View SolutionA beam of electrons whose kinetic energy is K emerges from a thin-foil "window" at end of an accelerator tube. A metal plate at distance d from this window is perpendicular to the direction of the emerging beam. (a) Show that we can prevent the beam from hitting the plate if we apply a uniform magnetic field such that
B≥√2mKe2d2
in which m and e are the electrons mass and charge
(b) How should →B be oriented?

View Solution
Knowledge Check
Two parallel beams of protons and electrons, carrying equal currents are fixed at a separation d. The protons and electrons move in opposite directions. There is a point P on the straight perpendicular line joining the two beams at a distance x from one beam. The magnetic field at this point is B. If B is plotted against x, it can be represented by the curve.
A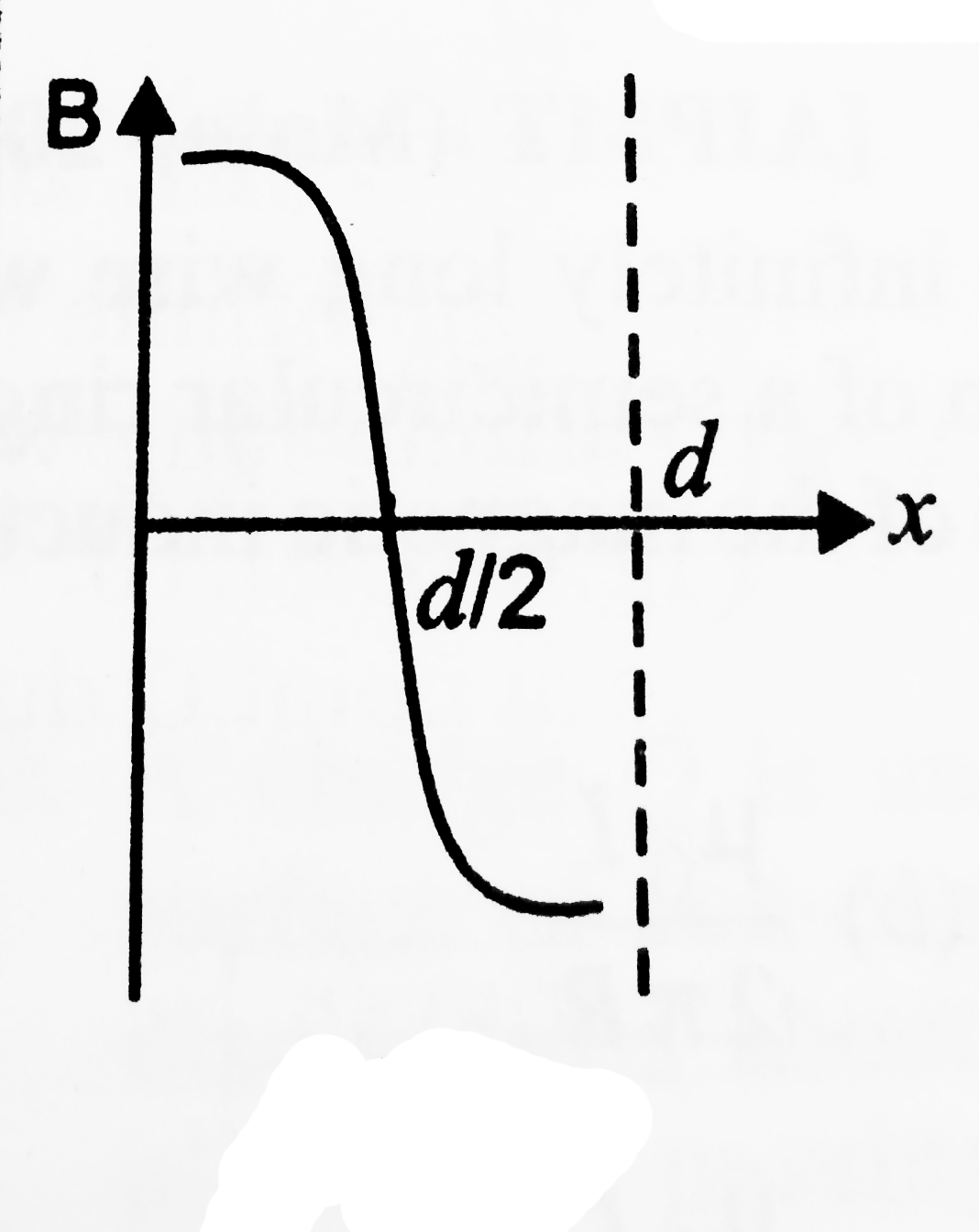 B
B C
C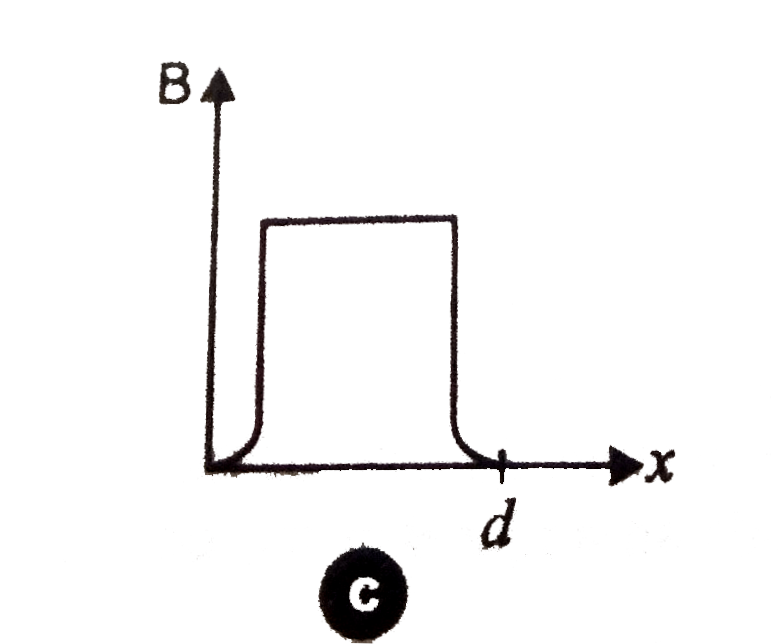 D
D
A beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionA beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionProtons having a kinetic energy of 50 eV are moving in the positive x-direction and enter a magnetic field B=0.5mˆkT directed out of the plane of the page and extending from x=0→x=1m as shown in Fig. 1.34.
a. Calculate the y-component of the protons' momentum as they leave the magnetic field.
b. Find the angle ϕ between the initial velocity vector of the proton beam and the velocity vector after the beam emerges from the field. Ignore relativistic effects and note that 1eV=1.60×10−19J.

View SolutionProtons having a kinetic energy of 5 MeV are moving in the positive x-direction and enter a magnetic field B=0.0500ˆkT directed out of the plane of the page and extending from x=0→x=1m as shown in Fig. 1.34.
a. Calculate the y-component of the protons' momentum as they leave the magnetic field.
b. Find the angle ϕ between the initial velocity vector of the proton beam and the velocity vector after the beam emerges from the field. Ignore relativistic effects and note that 1eV=1.60×10−19J.

View SolutionA proton and an alpha particle are projected in a perpendicular magnetic field B which exists in a region of width d, figure. Find the ratio of the sines of angles of deviation suffered by the proton and the alpha particle if before entering the magnetic field both the particles (i) have the same momentum (ii) have the same kinetic energy.
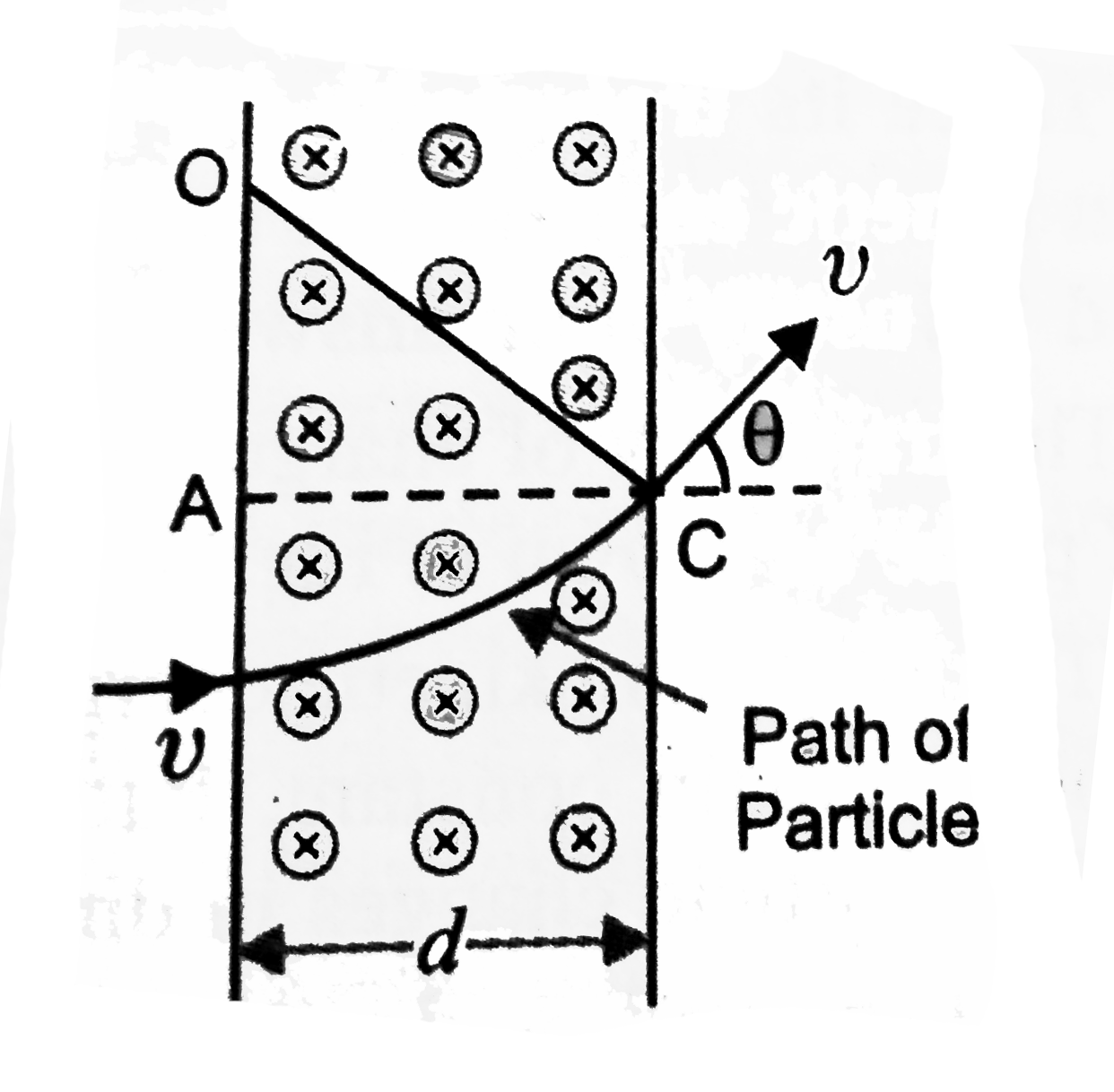
View SolutionA proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with E and B Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
View SolutionA proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with E and B Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
View Solution
