A proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic field with E and B Then the beam strikes a grounded target. Find the force imparted by the beam on the target if the beam current is equal to I .
To solve the problem of finding the force imparted by a proton beam on a grounded target when the beam passes through mutually perpendicular electric and magnetic fields without deviation, we can follow these steps:
Step 1: Understand the Forces Acting on the Proton Beam
The proton beam experiences two forces:
- The electric force (FE) due to the electric field (E).
- The magnetic force (FB) due to the magnetic field (B).
Since the beam passes without deviation, these forces must balance each other:
FE=FB
Step 2: Write the Expressions for the Forces
The electric force acting on a proton is given by:
FE=qE
where q is the charge of the proton.
The magnetic force acting on a proton moving with velocity v in a magnetic field is given by:
FB=qvB
Step 3: Set the Forces Equal
Since FE=FB, we can write:
qE=qvB
We can cancel q (the charge of the proton) from both sides (assuming q≠0):
E=vB
Step 4: Solve for Velocity
From the equation E=vB, we can express the velocity v of the protons:
v=EB
Step 5: Calculate the Total Current in the Beam
Let I be the current of the proton beam. The current can be expressed in terms of the number of protons n, the charge of a single proton e, and the velocity v:
I=n⋅e⋅v
Step 6: Substitute for Velocity
Substituting v=EB into the current equation:
I=n⋅e⋅EB
From this, we can express n:
n=IBeE
Step 7: Calculate the Force on the Target
The force F imparted by the beam on the target can be calculated using the momentum change per unit time. The momentum p of the beam is given by:
p=n⋅m⋅v
where m is the mass of a proton. The rate of change of momentum (force) is:
F=dpdt=n⋅m⋅d(v)dt+v⋅dndt
However, since v is constant and we are considering a steady beam, we can simplify this to:
F=n⋅m⋅v
Step 8: Substitute for n and v
Substituting n=IBeE and v=EB:
F=(IBeE)⋅m⋅(EB)
This simplifies to:
F=I⋅me
Final Result
Thus, the force imparted by the proton beam on the grounded target is:
F=I⋅me
The proton beam experiences two forces:
- The electric force (FE) due to the electric field (E).
- The magnetic force (FB) due to the magnetic field (B).
FE=FB
The electric force acting on a proton is given by:
FE=qE
where q is the charge of the proton.
FB=qvB
Since FE=FB, we can write:
qE=qvB
We can cancel q (the charge of the proton) from both sides (assuming q≠0):
E=vB
From the equation E=vB, we can express the velocity v of the protons:
v=EB
Let I be the current of the proton beam. The current can be expressed in terms of the number of protons n, the charge of a single proton e, and the velocity v:
I=n⋅e⋅v
Substituting v=EB into the current equation:
I=n⋅e⋅EB
From this, we can express n:
n=IBeE
The force F imparted by the beam on the target can be calculated using the momentum change per unit time. The momentum p of the beam is given by:
p=n⋅m⋅v
where m is the mass of a proton. The rate of change of momentum (force) is:
F=dpdt=n⋅m⋅d(v)dt+v⋅dndt
However, since v is constant and we are considering a steady beam, we can simplify this to:
F=n⋅m⋅v
Substituting n=IBeE and v=EB:
F=(IBeE)⋅m⋅(EB)
This simplifies to:
F=I⋅me
Thus, the force imparted by the proton beam on the grounded target is:
F=I⋅me
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point54videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together75videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
Similar Questions
A non-relativistic proton beam passes without deviation through a region of space where there are uniform transverse mutually perpendicular electric and magnetic fields with E=120kVm−1andB=50mT. Then the beam strikes a grounded target. Find the force which the beam acts on the target if the beam current is equal to i=0.8mA.
Mass of protons =1.67×10−27kg.View SolutionProtons move rectilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields E and B. The trajectory of protons lies in the plane xz as shown in the figure and forms an angle 9 with x-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
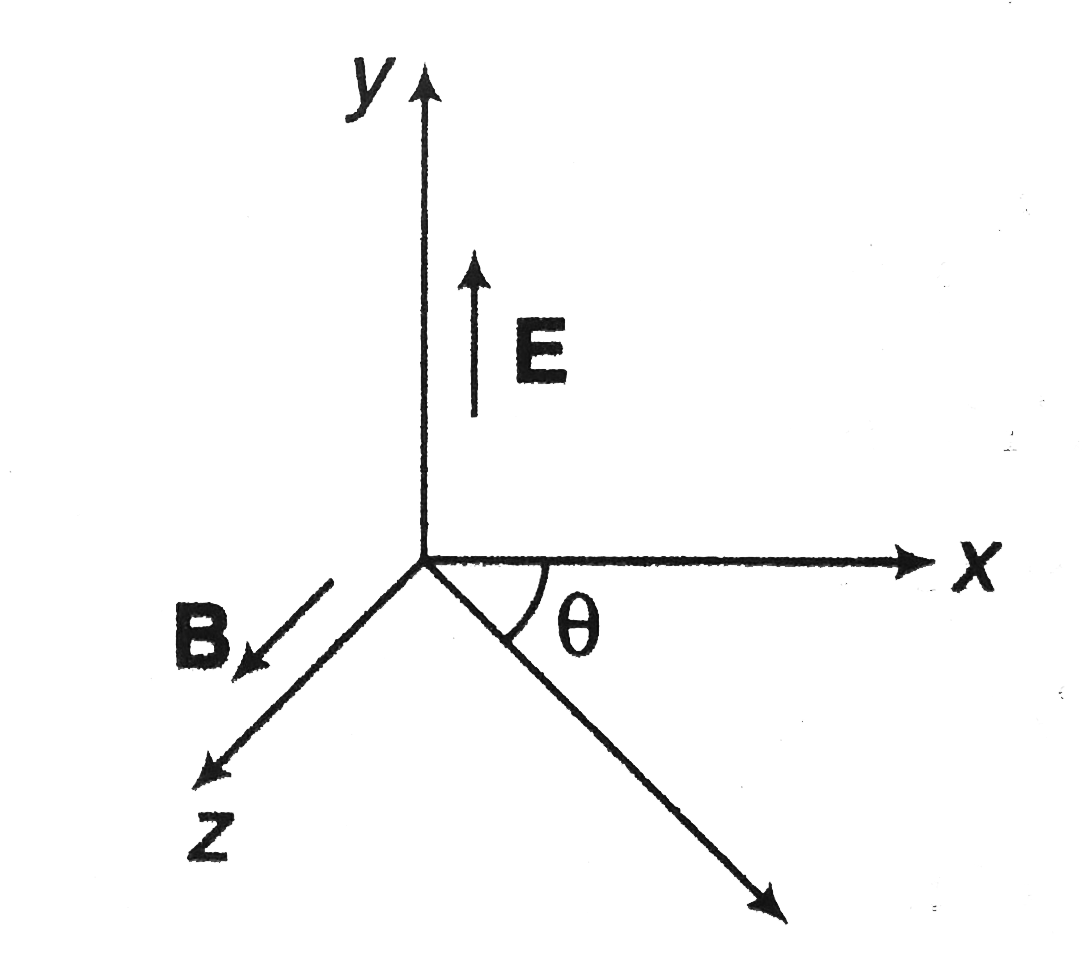 View Solution
View SolutionNon-relativistic protons move reactilinearly in the region of space where there are uniform mutually perpendicular electric and magnetic fields with E and B. The trajectory of the protons lie in the plane X-Y as shown in Fig. 1.107 and forms an angle ϕ with X-axis. Find the pitch of the helical trajectory along which the protons will move after the electric field is switched off.
 View Solution
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA beam of electrons passes undeflected through uniformly perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained then the electrons move:
View SolutionAn electron enters a region where magnetic field (B) and electric field (E ) are mutually perpendicular, then
View SolutionA proton moving with a constant velocity passes through a region of space without any changing its velocity. If E and B represent the electric and magnetic fields, respectively. Then, this region of space may have
View SolutionA proton moving with a constant velocity passes through a region of space without any changing its velocity. If E and B represent the electric and magnetic fields, respectively. Then, this region of space may have
View SolutionA beam of electrons is moving with uniform velocity in a region having transverse uniform electric and magnetic field of strength. 100 V/m and 0.1 T respectively at right angles to the direction of beam. The velocity of the electrons is
View Solution

