The given Venn diagram represents the sports preferences of a group of college students. There are three games. A Basketball, B-Football and C-Volleyball. Based on the diagram, how many play exactly one game? 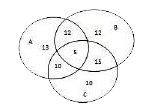
5
17
35
44
The correct Answer is:C
Step by step video & image solution for The given Venn diagram represents the sports preferences of a group of college students. There are three games. A Basketball, B-Football and C-Volleyball. Based on the diagram, how many play exactly one game? by Reasoning experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
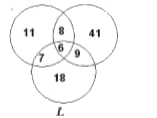
The above Venn diagram represent the students who play 3 sports M, N and L in a class. Total number of students who play game M is :A7B11C32D21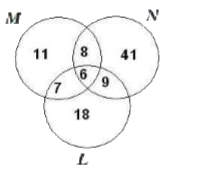
The above venn diagram represent the students who play 3 sport M,N and L in a class:
Total number of students who play game N is:A41B64C23D9The diagram below represents the students who play cricket, football and kabaddi

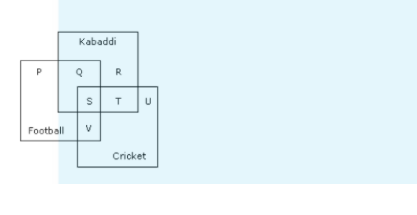
Seeing the diagram indicate the students who play all the 3 games.AA+B+CBG + ECD + E + GDD
The given Venn diagram represent the number of students in a class who study three languages, French Spanish and Japanese.
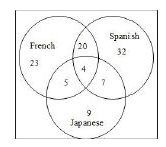
The number of students studying French, Spanish and Japanese is:
View SolutionIn a class of 35 students, 24 students like cricket and 16 like football. If each student plays atleast one game, find how many students like both games ?
View SolutionThe bar graph given below represents the number of players of a college taking part in three games for 3 years.

The number of players playing football in 2016 is how much per cent less than the players playing football in 2014?
View SolutionThe given Venn diagram shows the number of students who have passed in the three exams, viz, english, science and Maths. How many students failed in all the three exams?
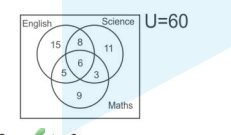
View SolutionThe given Venn diagram shows a total of 50 students who appeared for three different examinations : A, B, and C. All have appeared for at least one examination. How many appeared for examination A and B but not C ?
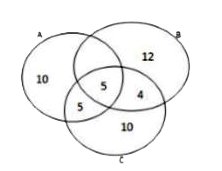
View Solution