An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle a with the vertical, the maximum possible value of cis given by :
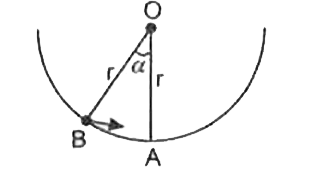
cota=3
tan a = 3
sec a= 3
cosec c = 3.
The correct Answer is:A
Topper's Solved these Questions
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Recent Competitive Questions
3 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- UNIT TEST -06BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST -06EXERCISE - Multiple Choice Questions
19 Videos
Similar Questions
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View Solution
Knowledge Check
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline then
View Solution
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline then
View Solution
