A heavy small sized sphere is suspended by a string of length /. The sphere is rotating in a horizontal circle of certain radius 'r making an angle with the vertical forming a conical pendulum. What is the time period of the pendulum ?
t=2π√lsinθg
t=√lsinθg
t=2π√lg
t=2π√ltanθg
The correct Answer is:B
Topper's Solved these Questions
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Recent Competitive Questions
3 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- UNIT TEST -06BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST -06EXERCISE - Multiple Choice Questions
19 Videos
Similar Questions
A heavy & big sphere is hang with a string of length l. This sphere move in a horizontal circular path making an angle θ with vertical then its time period is
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will the pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force?
View Solution
Knowledge Check
A heavy small sized sphere is suspended by a string of length 2. The sphere is rotated uniformly in a horizontal circle with the string making an angle θwith the vertical. The time period of this conical pendulum is
A2π√ltanθgB2π√lcosθgC2π√1gD2π√lcosθgA heavy small sized sphere is suspended by a string of length l . The sphere rotates uniformly in a horizontal circle with the string making an angle θ with the vertical. Then the time period of this conical pendulum is-
AT = 2πBT=2π√(lsinθg)CT=2π√(lcosθg)DT=2π√(lg)A heavy & big sphere is hang with a string of length l. This sphere move in a horizontal circular path making an angle θ with vertical then its time period is
AT=2π√lgBT=2π√lsinθgCT=2π√lcosθgDT=2π√lgcosθ
A sphere of mass 200 g is attached to an inextensible string of length 130 cm whose upper end is fixed to the ceilling . The sphere is made to describe a horizontal circle of radius 50 cm Calculate the periodic time of this conical pendulum and the tension in the string .
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View SolutionA particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
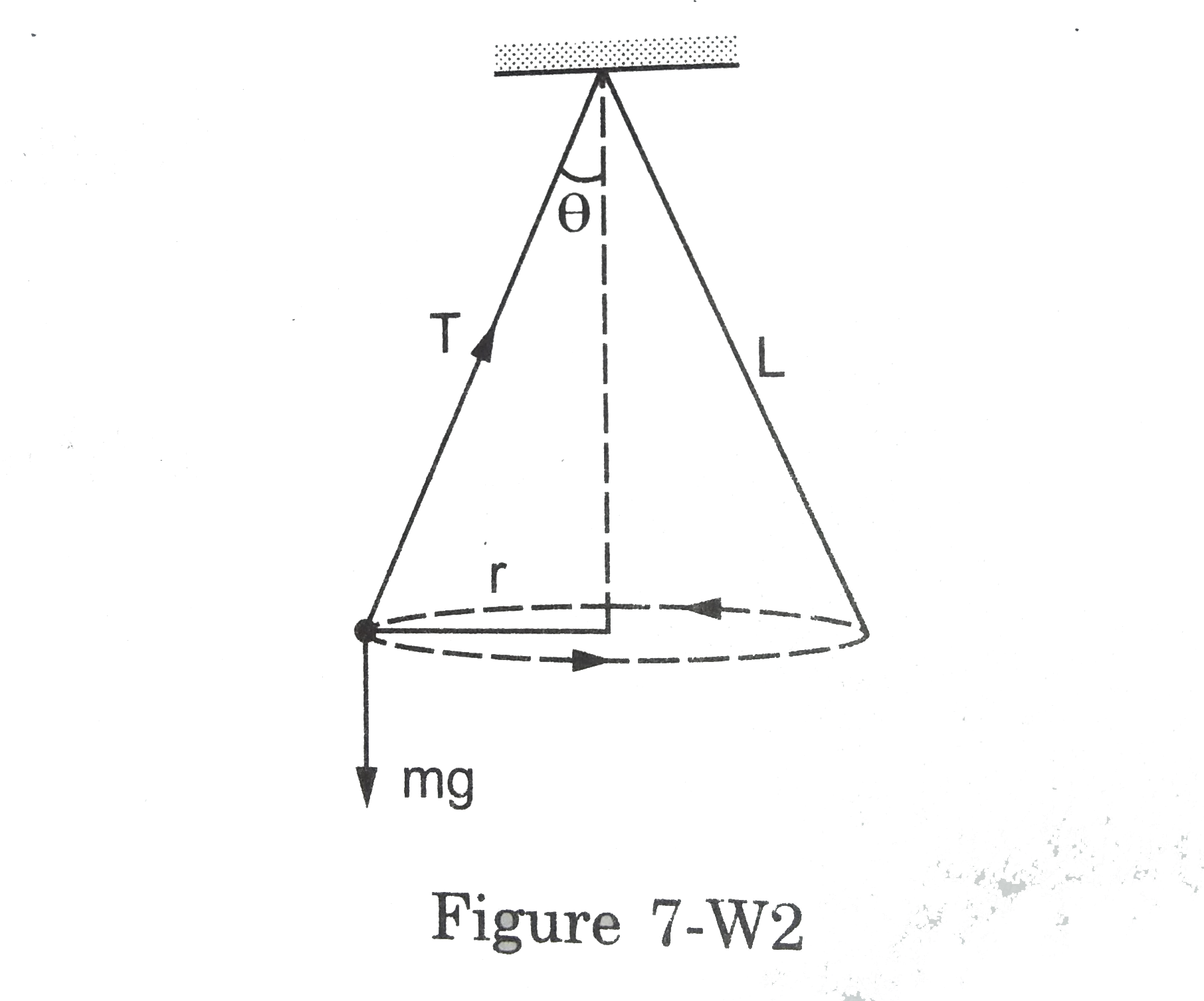
.
View Solution
