A network of resistors is connected to a 16 V battery with internal resistance of 1Ω, as shown in figure.
a. Compute the equivalent resistance of the network.
b. Obtain the current in each resistor.
Obtain the voltage drops VABVBCandVCD
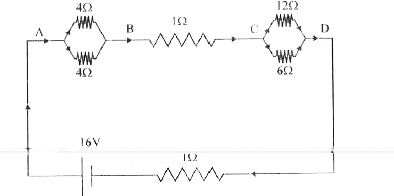
a.4Ω and 4Ω resistor are parallel ,R1=[(4×4)(4+4)]=2Ω
The 12Ω and 6Ω resistors in parallel," "∴R2=[12×612+6]=4Ω.
The equivalent resistance R of the network is obtained by combining these resistor (2Ωand 4Ω) with 1Ω series that is R=2Ω+4Ω+1Ω=7Ω.
(b) The total current I in the circuit isI=εR+r=16V(7+1)Ω=2A
Consider the resistors between Aand B. If I1 is the curent is the one of the of 4Ω resitors and I1 the current in the order ,
I1×4=I2×4 i.e.,I1=I2, which is otherwise obvious from the symmetry of the two arms.
But I1+I2=I=2A,I1=I2=IA
i.e., current in each 4 resistor is lA. Current 1 resistor between B and C would be 2A. Now consider the resistance between Cand D.If I3 is the curent is the 12Ω resistor , and I4 in the 6Ωresistor I3×12=I4×i.e.,I4=2I3
But I3+I4=2A
Thus I3=(23)A,I4=(43)A
i.e., the current in the 12Ω resistor is (23)A, while the current in the 6Ω resistor is (43)A.
(c) The voltage dreop across AB is VAB=I1×4=IA×4Ω=4V
The voltage dreop across BC is VBC=2A×1Ω=2V
The voltage dreop across CDis VCD=12Ω×I3=12Ω×(23)A=8V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - SOLUTION TO EXERCISES FROM NCERT TEXT
24 Videos
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT
25 Videos
- ATOMSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ATOMSEXERCISE - COMPETITIVE EXAM CORNER
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NEW JOYTHI PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITIVE EXAM CORNER
15 Videos
Similar Questions
A network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
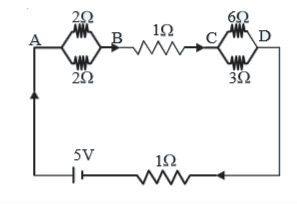
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD

View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1Ω as shown in figure. (a) Compute the equivlaent resistance of the network. (b) Obtain the current in each resistor and (c ) obtain the voltage dropVAB,VBC and VCD.
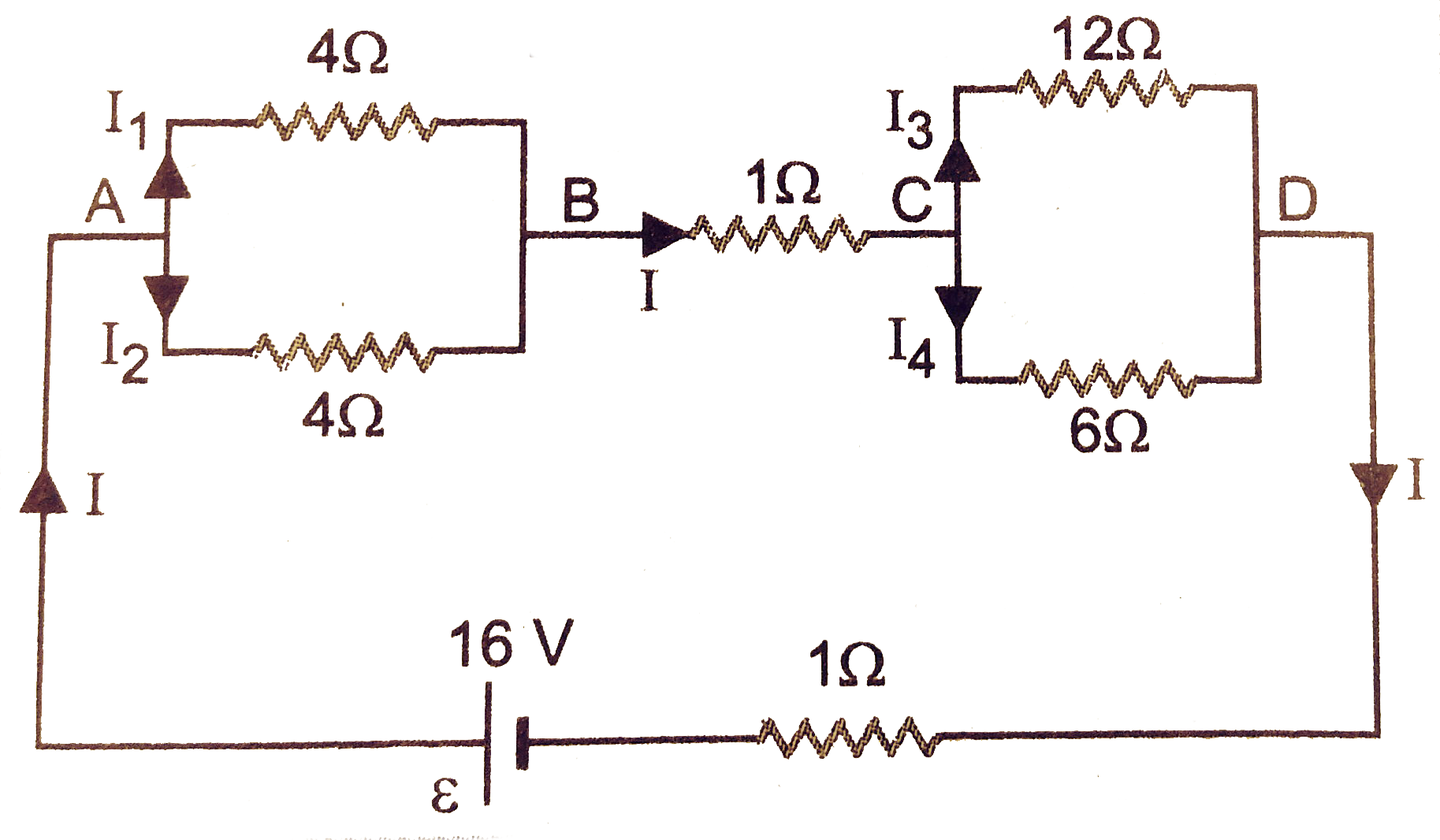
View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1Ω, as shown in Fig. 4.33.

(a) Compute epuivalent resistance of the network,
(b) obtain the current In in each resistor, and
(c ) obtain the voltage drops VAB,VBC and VCD.
View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1Ω, as shown in Fig. 4.33.

(a) Compute epuivalent resistance of the network,
(b) obtain the current In in each resistor, and
(c ) obtain the voltage drops VAB,VBC and VCD.
View Solution
A network of resistors is connected to a battery of negligible internal resistance, as shown in figure. Calculate the equivalent resistance between the point A and D, and the value of the current I3.
View SolutionA network of resistors is connected to a 16V battery as shown in the following figure. Compute the equivalent resistance of the network.
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View Solution
