A cell of emf E and internal resistance r is connected to an external resistance R. Show that at maximum power transfer, R =r
Power =I3R=(ER+r)2.R
To find the variations w.r.to R, ddR[(ER+r)2.R]=0
∴E2ddRR(R+r)2=0 ∴ddRR(R+r)2= ∴(R+r)2×1−R×2(R+r)(R+r)4=0
∴R+r−2R=0 ∴R=r
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - COMPETITIVE EXAM CORNER
37 Videos
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT
25 Videos
- ATOMSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ATOMSEXERCISE - COMPETITIVE EXAM CORNER
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NEW JOYTHI PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITIVE EXAM CORNER
15 Videos
Similar Questions
A cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View SolutionA cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, versesR.
View Solution
Knowledge Check
A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)nA cell of internal resistance r connected across an external resistance R can supply maximum current when
AR=rBR>rCR=r2DR=0A cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
A1/nB1/(n+1)Cn/(n+1)D(n+1)/n
A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, verses 'R.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P ) vs load resistance ( R ) graph.
View Solution(a) A cell of emf E and internal resistance r is connected to a resistance R.
(i) Relate r and R, so that power in R is maximum.
(ii) Maximum power consumed by R.
(iii) Efficiency.
(b) Find value r in terms of R so that power in external circuit is maximum.
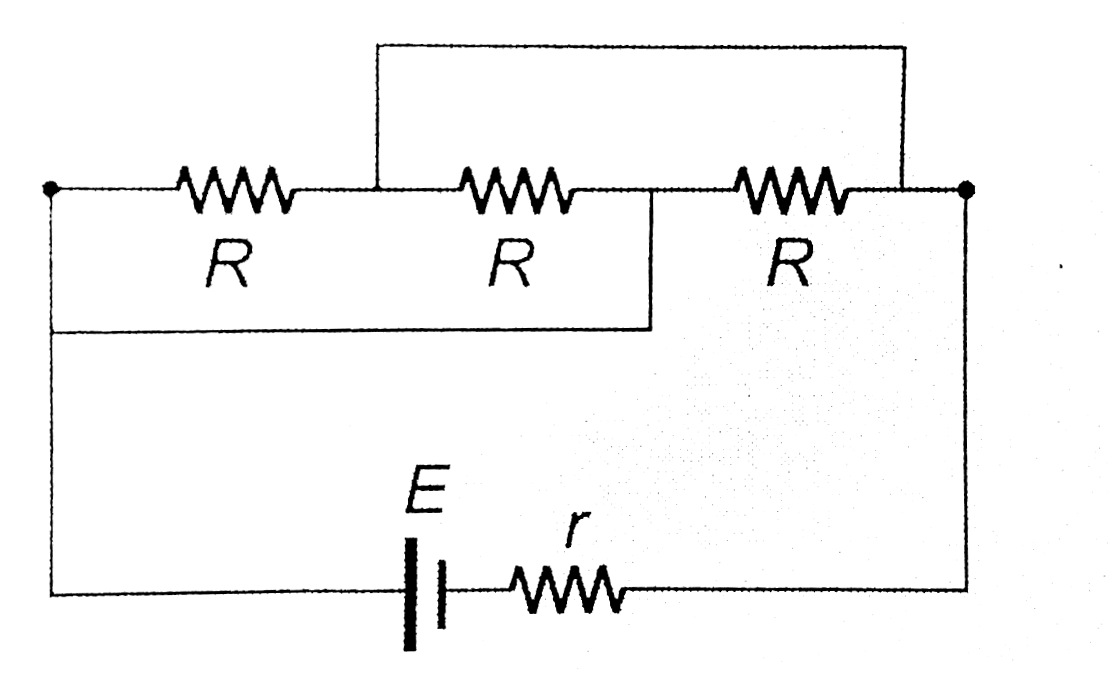
(c) A battery of internal resistance 4Ω is connected to the network of resistance as shown in the figure. what must be the value of R so that maximum power is delivered to the network? what is tha maximum power?

View Solution
