Twelve equal resistors each of resistance 12Ω form edges of a cube as shown. A battery of emf 24 volts is connected across the diagonally opposite corners of this cube. Deter mine the equivalent resistance and current through each edge.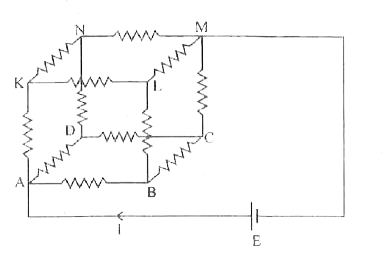
By symmetry, the current through the
paths AB, AD & AK is equal to13 . In
the same way current through the paths BC, BL, DC, DN, KL, KN is equal to16 and through the paths CM, LM, NM is equal to 13Let Req the equivalent resistance. Using Kirchhoff.s voltage law for the mesh ABCMEA,13×AB+16BC+13CM=E
i.e.,13R+IR6+IR3=E
5IR6=E...........(1)
But Req=EI=5IR6I=56R SinceR=12ΩReq=56×12=10Ω
E=24V ∴I=EReq=2410=2.4A
Hence current through the branches, AB, AD, AK and CM, LM, NM =2.43= 0.8 A and through BC, BL, DC, DN, KL & KN = 2.46 = 0.4 A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - COMPETITIVE EXAM CORNER
37 Videos
- CURRENT ELECTRICITYBOOK - NEW JOYTHI PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT
25 Videos
- ATOMSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ATOMSEXERCISE - COMPETITIVE EXAM CORNER
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NEW JOYTHI PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITIVE EXAM CORNER
15 Videos
Similar Questions

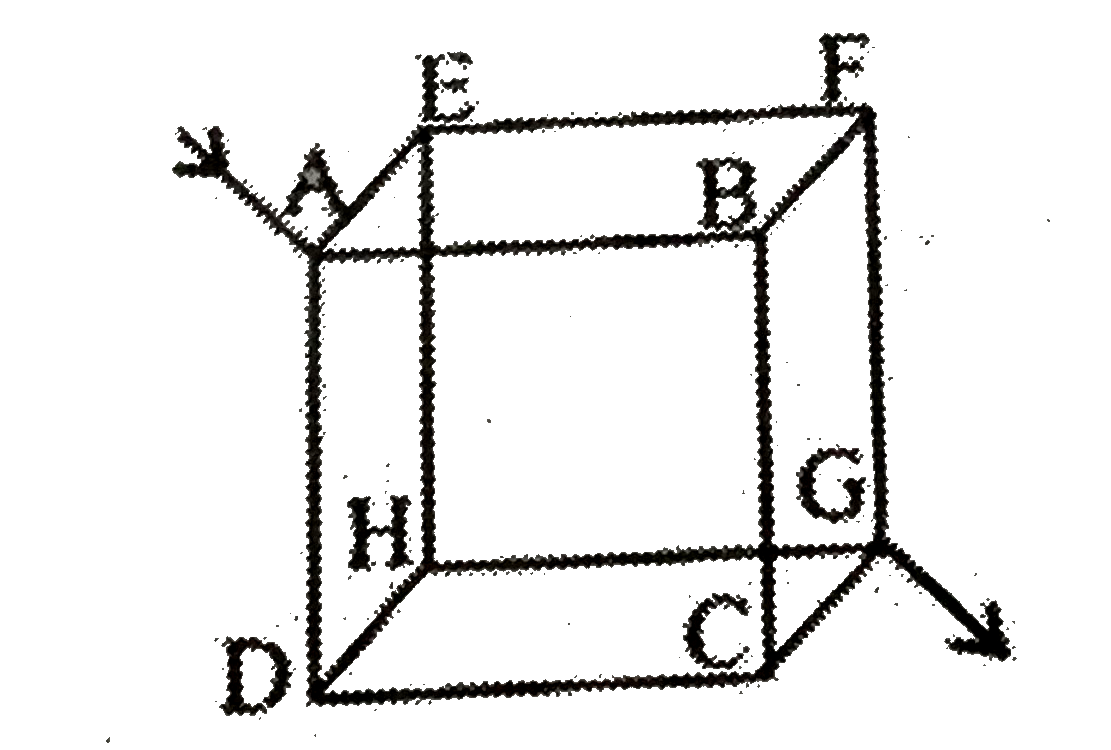
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View Solution
Knowledge Check
Twelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4ATwelve wires each of resistance 6Ω are connected to from a cube as shown in the adjoining figure. The current enters at a cornet A and leaves at erhe diagonally opposite corner G. The equivalent resistance across the corners A and G is
 A12ΩB6ΩC3ΩD5Ω
A12ΩB6ΩC3ΩD5ΩTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10Ω
A battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
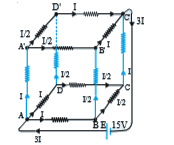
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω . Determine the equivalent resistance of the network and the current along each edge of the cube.

View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View SolutionTwelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View Solution
