In the molcule OA=C=OB , the formal charge on OA ,C and OB are respectively :
−1,0,+1
+1,0,−1
−2,0,+2
0,0,0
The correct Answer is:D
Similar Questions
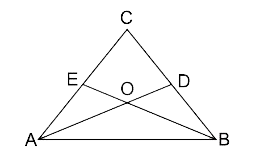
In the given figure ∠ABC=∠BAC , D and E are pointts on BC and AC respectively such that DB = AE . If AD and BE intersect at O then prove that OA = OB
View SolutionIf the tangent drawn at any point P(acos4θ,asin4θ) on the curve √x+√y=√a meets the co-ordinate axes in A and B respectively then
Q: The value of OA−OBOA+OB is (where O is origin)
View Solution
Knowledge Check
A plane makes intercepts OA, OB, OC whose measures are a, b, c on the axes x, y, z respectively. The area of the triangle ABC is
A12√a2+b2+c2B12√b2c2+c2a2+a2b2C12√ab+bc+acD11√a2b+b2c+c2a
Tangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
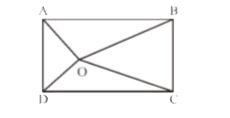
View SolutionO is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
View SolutionTwo fixed point AandB are taken on the two axes such that OA=a,OB=b, two variable points C,D are taken on the same axes respectively, find the locus of the point of intersection of ADandCB if : 1OC−1OD=1OA−1OB
View SolutionThe resultant of two forces →P and →Q acting at O at →R . If any traversal cuts them at A,B and C, respectively, show that POA+QOB=ROC
View SolutionIf the tangent drawn at any point P(acos4θ,asin4θ) on the curve √x+√y=√a meets the co-ordinate axes in A,B respectively then. The value of OA−OBOA+OB is (where O is origin)
View SolutionPoint A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionIf O is the origin and the coordinates of A and B are (51, 65) and (75, 81), respectively. Then OA×OBcos∠AOB is equal to
View Solution
