Establish Ampere-Maxwell's law
∮B.dl=μ0ic+ε0dϕEdt.
Ampere-Maxwell.s Law Consider a parallel plate capacitor with circular plates. When the capacitor is charged, the electric field E in space between the two plates increases at a rate dEdt, which means that the charge must be supplied to the plates of the capacitor, for this purpose a current has to flow towards the positive plate and a current must leave the negative plate.
As the electric field is changing, an induced magnetic field is set up [(Fig. (a)]. Faraday.s law of electromagnetic induction,
∫E.dl=dϕBdt
Similar to the Faraday.s law for induced magnetic field, ∫B.dl=μ0ε0dϕεdt
where, ϕE=∫E.ds ......(i)
According to Ampere.s circuit theorem,
∫B.dl=μ0ic .......(ii)
Here, ic is the conduction current passing through a closed loop around which the line integral is taken.
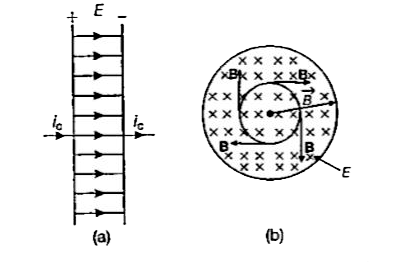
So, it is clear that there are two ways of setting up a magnetic field
(a) by passing current through a wire and
(b) by changing the electric field.
Allowing for both the possibilities, in general
∫B.dl=μ0ic+μ0ε0dϕEdt
Similar Questions
(A) : A magnetic field is produced either by a steady current or by a time varying electric field (R) : According to Ampere’s law ∮¯¯¯B.¯dl=μ0i0+μ0ε0d∮Edt
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Match the statements in Column I labeled as (a), (b), (c), and (d) with those in Column II labeled as (p), (q), (r), and (s).Any given statement in Column I can have correct matching with one or more statements in Column II.
Column IColumn II(a)∮→E.d→s=−dϕBdt(p)Maxwell's law of induction(b)∮→B.d→s=μ0ε0dϕEdt(q)Ampere-Maxwell law(c)∮→B.d→s=μ0Ienc(r)Ampere's law(d)∮→B.d→l=u0ε0dϕEdt+μ0Ienc(s)Faraday's law of indcutionA2.8×10−8s−1B3.2×10−8s−1C6×1011s−1DNone of these - Question 2 - Select One
Dimensions of ε0dϕEdt are same as that of
A[AT]B[A]C[ML2T−2]D[ML−1T−2] - Question 3 - Select One
The maxwell’s equation :
∮→B.→dl=μ0(i+ɛ0.dϕEdt) is a statement of -AFaraday’s law of inductionBModified Ampere’s lawCGauss’s law of electricityDGauss’s law of magnetism
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
 View Solution
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
 View Solution
View SolutionIn each question, there .is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Eac!h question bas 4 options (a), (b), (c) and (d), ONLY ONE of these four options is correct.
In the given table, Column I shows different laws in electromagnetic theory, Column II shows the related physica l quantities and Column III shows the equations related to the different laws.
Column IColumn IIColumn II(I) Gauss's law(i)Magnetism (J)∮→B.d→s=μ0ε0dϕEdt+μ0dqdt(II)Ampere's law(ii)Current (K) ∮→B.d→A=0(III)Gauss's law (iii)Induction (L)∮→E.d→s=dϕBdt(IV)Faraday's (iv)Electricity (M)∮→E.d→A=qε
In which law does the charge create diverging electric fields?View SolutionIn each question, there .is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Eac!h question bas 4 options (a), (b), (c) and (d), ONLY ONE of these four options is correct.
In the given table, Column I shows different laws in electromagnetic theory, Column II shows the related physica l quantities and Column III shows the equations related to the different laws.
Column IColumn IIColumn II(I) Gauss's law (i) Magnetism (J)∮→B.d→s=μ0ε0dϕEdt+μ0dqdt(II)Ampere's law(ii)Current (K) ∮→B.d→A=0(III)Gauss's law (iii)Induction (L)∮→E.d→s=dϕBdt(IV)Faraday's (iv)Electricity(M)∮→E.d→A=qε
Jn which law there are no magnetic monopoles invo lved?View SolutionIn each question, there .is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Eac!h question bas 4 options (a), (b), (c) and (d), ONLY ONE of these four options is correct.
In the given table, Column I shows different laws in electromagnetic theory, Column II shows the related physica l quantities and Column III shows the equations related to the different laws.
Column IColumn IIColumn II(I) Gauss's law (i) Magnetism (J)∮→B.d→s=μ0ε0dϕEdt+μ0dqdt(II)Ampere's law(ii)Current (K) ∮→B.d→A=0(III)Gauss's law (iii)Induction (L)∮→E.d→s=dϕBdt(IV)Faraday's (iv)Electricity(M)∮→E.d→A=qε
In which law currents or changing electric fi elds(E's) make circulating magnetic fields (B's)?View Solution

