A body of weight W is suspended from a rigid support P by means of a massless string as shown in figure. A horizontal force F is applied at point O of the rope. The system is in equilibrium when the string makes an angle θ with the vertical. If the tension in the string is T,
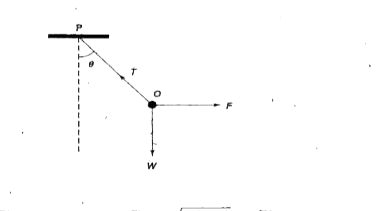
F=Tsinθ
W=Tsinθ
T= √W2+F2
F=W tantheta
The correct Answer is:A, C, D
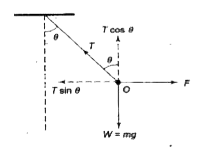
The mass in equilibrium at point O under the action of the concurrent forces F, T and W =mg.,Therefore, as shown in figure, the horizontal component T sin θ tension T must-balance with force F and the vertical component T cos θ must balance with weight W =mg. Thus F=Tsinθ ---------(i)
and W=Tcosθ ---------ii)
Squaring Eqs. (i) and (ii) and adding we get T2=W2+F2
Dividing (i) by (ii) we get F=Wtanθ.
Similar Questions
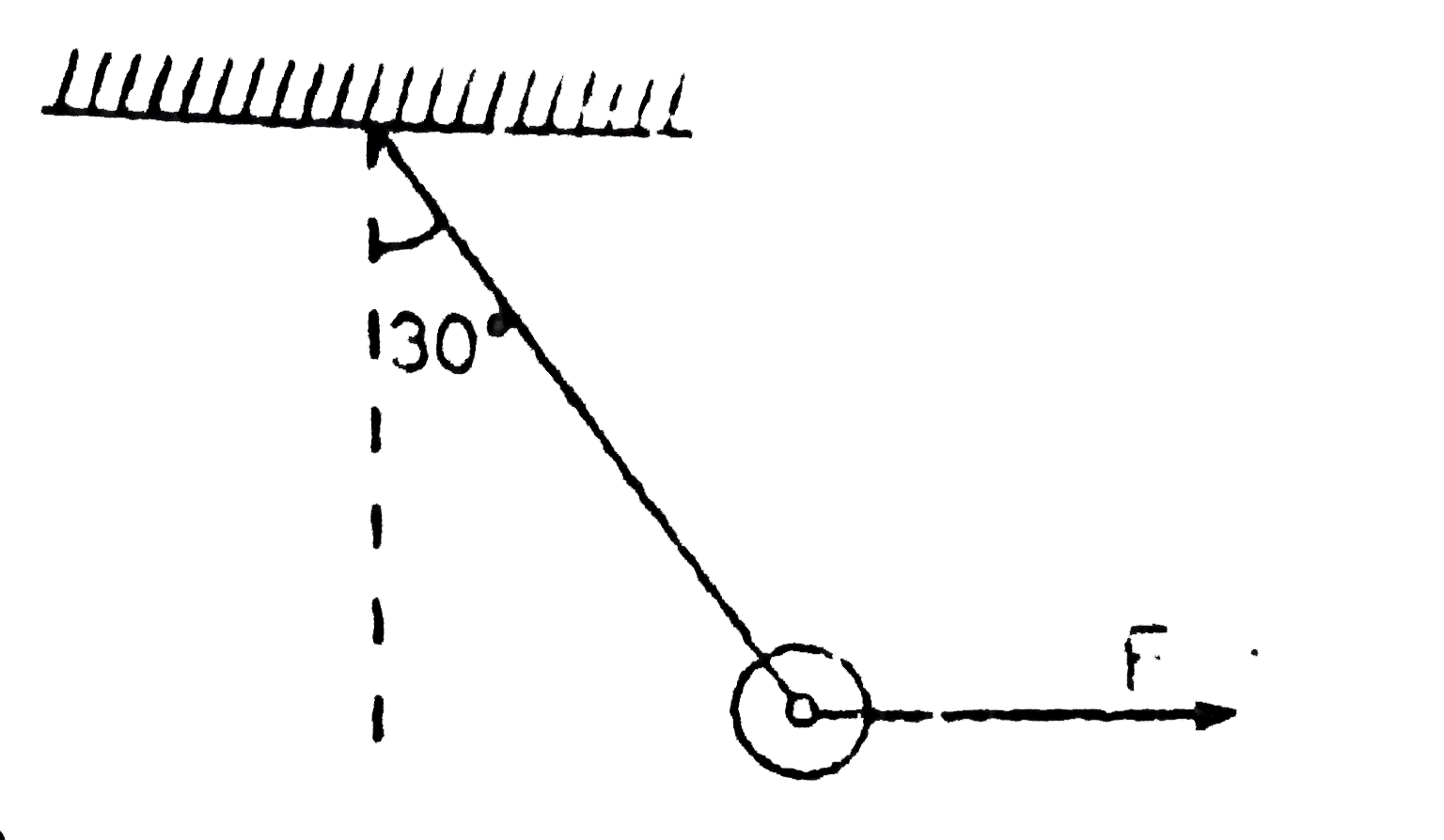
A heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
 .
.
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
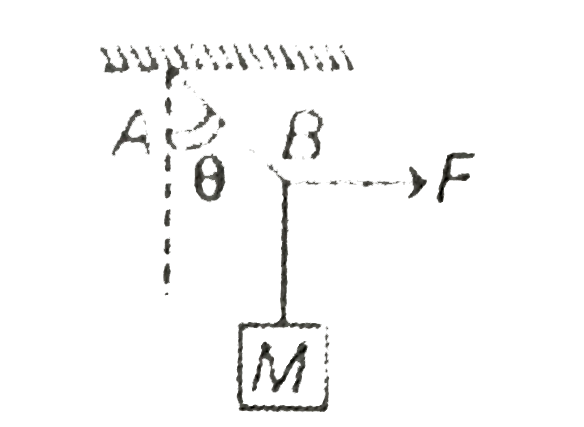
View Solution
Knowledge Check
A heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
 .A10NB10√3NC5ND10√3N
.A10NB10√3NC5ND10√3NA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
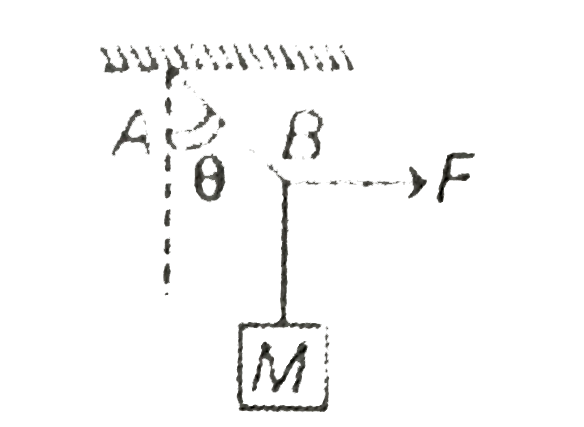 AF sinθBF/sinθCFcosθDF/cosθ
AF sinθBF/sinθCFcosθDF/cosθA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)
A body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
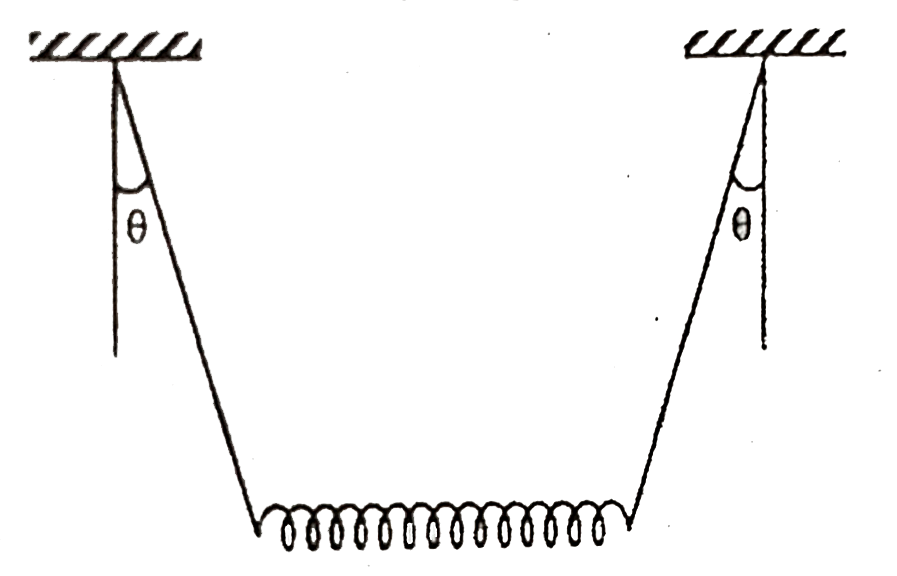
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.

View Solution
