If a, b, c, d, e,f are in A.P., then e - c is equal toSolution in Punjabi
2(c -a)
2(f-d)
2(d-c)
d-e.
Step by step video & image solution for If a, b, c, d, e,f are in A.P., then e - c is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Write the first three terms of the sequence defined by the following :
an=n(n+2).
View SolutionIf A = { a, b,c}, B = {p,q}, find B×A .
View SolutionWhich of the following are sets ? Justify your answer. The collection of all the months of a year beginning with the letter J.
View SolutionIf a,b,c,d,e,f are in ..., then e-c is equal to
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
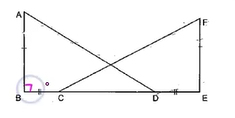
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
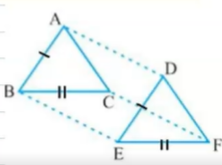
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View SolutionThe H.C.F. of ab,cd,ef is equal to (a) LCMof a, c, eHCFof b, d, f (b) HCFof a, c, eLCMof b, d, f (c) HCFof a, c, eHCFof b, d, f (d) acebdf
View SolutionIn Figure, DE∣∣AC and DF∣∣AE . Prove that EFBF=ECBE .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of △ABC. Then DEF is congruent to triangle.
(a)ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
View SolutionIn Figure, AB⊥BE and FE ⊥BE. If BC=DE and AB=EF, then ABD is congruent to: EFC (b) ECF (c) CEF (d) FEC
View SolutionIf a,b,c,d,e,f are in A.P. then d−b= ……
View Solution
