C1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Prove that the centroid of the triangle PAB lies on C1 .Solution in Punjabi
Step by step video & image solution for C_1 and C_2 are two concentric circles, the radius of C_2 being twice that of C_1. From a point P on C_2, tangents PA and PB are drawn to C_1. Prove that the centroid of the triangle PAB lies on C_1 . by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Determine whether the following represents a circle, a point or no circle :
1−x2−y2=0.
View SolutionEvaluate the following:
i51.
View SolutionExpand (1−x2)−1/2 when | x | < 2.
View SolutionC0C1+C1C2+C2C3+…+Cn−1Cn=
View SolutionIf (C0+C1)(C1+C2)…(Cn−1+Cn)=kC0C1C2…Cn then k=
View SolutionTwo solutions whose concentrations are c_1 and c_2 are and c_1 lt c_2 then the order of osmotic pressure is-
View SolutionLet C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of C
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View SolutionTransverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
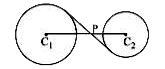
View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
(i) 18 (ii) 20 (iii) 12 (iv) 15
View SolutionThe centres of two C1 and C2, each unit of unit radii, are at a distance of 6 units from each other. Let P be the mid-point of the line segment joining the centres of C1andC2. A third circle C is drawn such that it is externally tangent to both the circles C1andC2 at the same points where the lines passing through P are tangent to the circles C1andC2. The radius of the circle C is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionIn the ambiguous case, if a,bandA are given and c1,c2 are the two values of the third (c1−c2)2+(c1+c2)2tan2A is equal to
View SolutionC1andC2, are the two concentric circles withradii r1andr2,(r1<r2). If the tangents drawnfrom any point of C2, to C1, meet again C2, at theends of its diameter, then
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View Solution
