A block 1 of mass $m_{1}$ , constrained to move along a plane inclined at angle $θ$ to the horizontal, is connected via a massless inextensible string that passes over a massless pulley, to a second block 2 of mass $m_{2}$ . Assume the coefficient of static friction between the block and the inclined plane is $μ_{k}$ and the coefficient of kinetic friction is $μ_{k}$

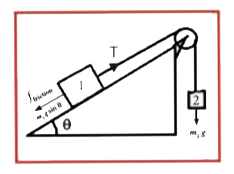
What is the relation between the masses of block 1 and block 2 such that the system just starts to slip?

Text Solution

Verified by Experts

By the principle of homogeneity, $a / V^{2}$ is of the dimensions of pressure and b is of the dimensions of volume.
[a] = [pressure] $[V^{2}] = [M L^{- 1} T^{- 2}] [L^{6}] = [M L^{5} T^{- 2}]$
[b] $= [V] = L^{3}$

Updated on:21/07/2023

A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is $μ$ then
.
A $μ > tan θ$
B $f = m g sin θ$
C $f = μ m g cos θ$
Dthe reaction of the ground on the block is mg cos $θ$
A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
A2 kg
B4 kg
C1.6 kg
D2.5 kg
Two block of masses $m 1$ and $m 2$ are connected with a massless unstretched spring and placed over a plank moving with an acceleration $' a'$ as shown in figure. The coefficient of friction between the blocks and platform is $μ$

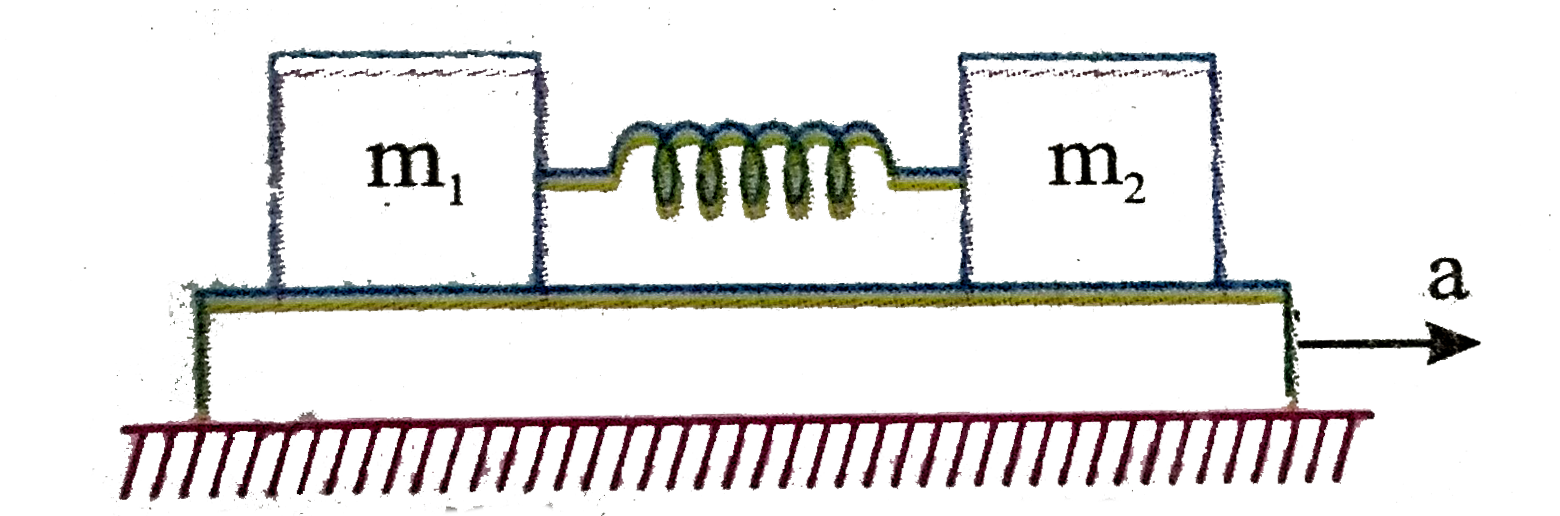Aspring will be stretched if $a > μ g$
Bspring will be commpressed if $a \leq μ g$
Cspring will neither be compressed nor be stretched for $a < μ g$ only.
Dspring will be in its natural length under all conditions.