Coefficient of kinetic friction and coefficient of static friction between two blocks is μk and μs respectively. In general
μs<μk
μs>μk
μs=μk
None of these
To solve the question regarding the relationship between the coefficient of static friction (μ_s) and the coefficient of kinetic friction (μ_k), we can follow these steps:
1. Understanding Friction:
- Friction is the force that opposes the relative motion of two surfaces in contact. There are two types of friction to consider: static friction (when the surfaces are not moving relative to each other) and kinetic friction (when the surfaces are sliding past each other).
2. Defining Coefficients:
- The coefficient of static friction (μ_s) is defined as the ratio of the maximum static frictional force (F_s) to the normal force (N) acting on the object. Mathematically, it can be expressed as:
Fs≤μsN
- The coefficient of kinetic friction (μ_k) is defined as the ratio of the kinetic frictional force (F_k) to the normal force (N). It can be expressed as:
Fk=μkN
3. Limiting Friction:
- The maximum static frictional force before motion occurs is known as limiting friction (F_s,max). This is given by:
Fs,max=μsN
4. Kinetic Friction:
- Once the object starts moving, the frictional force acting on it is the kinetic friction, which is generally less than the maximum static friction:
Fk=μkN
5. Comparing the Two Coefficients:
- From the definitions and the behavior of friction, it is observed that:
Fs,max>Fk
- This implies:
μsN>μkN
- Since the normal force (N) is positive and non-zero, we can divide both sides by N:
μs>μk
6. Conclusion:
- Therefore, we conclude that the coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k). This is a general observation in physics.
Final Answer:
The coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k).
- Friction is the force that opposes the relative motion of two surfaces in contact. There are two types of friction to consider: static friction (when the surfaces are not moving relative to each other) and kinetic friction (when the surfaces are sliding past each other).
- The coefficient of static friction (μ_s) is defined as the ratio of the maximum static frictional force (F_s) to the normal force (N) acting on the object. Mathematically, it can be expressed as:
Fs≤μsN
- The coefficient of kinetic friction (μ_k) is defined as the ratio of the kinetic frictional force (F_k) to the normal force (N). It can be expressed as:
Fk=μkN
- The maximum static frictional force before motion occurs is known as limiting friction (F_s,max). This is given by:
Fs,max=μsN
- Once the object starts moving, the frictional force acting on it is the kinetic friction, which is generally less than the maximum static friction:
Fk=μkN
- From the definitions and the behavior of friction, it is observed that:
Fs,max>Fk
- This implies:
μsN>μkN
- Since the normal force (N) is positive and non-zero, we can divide both sides by N:
μs>μk
- Therefore, we conclude that the coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k). This is a general observation in physics.
The coefficient of static friction (μ_s) is greater than the coefficient of kinetic friction (μ_k).
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
The coefficient of static friction may be
View SolutionThe coefficient of static friction between two surfaces depend on
View SolutionDefine the coefficient of static friction and kinetic friction.
View SolutionIn Fig the block are at rest a force of 10N act on the block of 4kg mass .The coefficient of staic friction and the coefficient of kinetic friction are μs=0.2andμs=0.15 for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the 2kg and 4kg block in this situation is

View SolutionA force of 750 N is applied to a block of mass 102 kg to prevent it from sliding on a plane with an inclination angle 30∘ with the horizontal. If the coefficients of static friction and kinetic friction between the block and the plane are 0.4 and 0.3 respectively, then the frictional force acting on the block is
View Solution
A force F=2t is spplied at t=0 sec to the block of mass m placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are μS and μk respectively. Which of the following graphs best represents the acceleration vs time of the block(μS>μk)?
View Solution
A force F=2t is spplied at t=0 sec to the block of mass m placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are μS and μk rspectively. Which of the following graphs best represents the acceleration vs time of the block(μS>μk)?
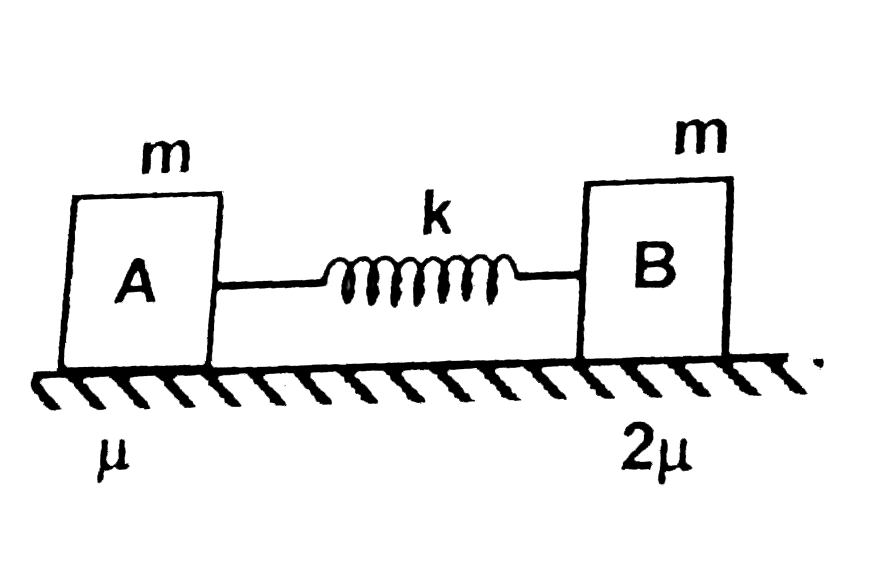
View SolutionTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View Solution
Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μS and μk respectively.
View Solution
