Use the diagram below to answer the following questions. 40 spheres of equal mass make two rings of 20 spheres each. The ring on the right has a radius twice as large as the ring on the left.

At what position could a mass be placed so that the gravitational force that it would experience would be the same from both rings?
A
B
C
D
The correct Answer is:b
Similar Questions
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
Knowledge Check
Use the diagram below to answer the following questions. 40 spheres of equal mass make two rings of 20 spheres each. The ring on the right has a radius twice as large as the ring on the left.
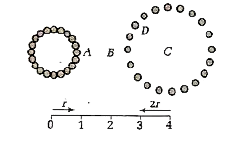
At what position could a mass be placed so that the net gravitational force that it would experience would be zero?AABBCCDDUse the diagram below to answer the following questions. 40 spheres of equal mass make two rings of 20 spheres each. The ring on the right has a radius twice as large as the ring on the left.
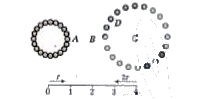 If the position of the spheres approximates two uniformly dense rings, which of the following is the concerning a mass placed at position D?AThe net gravitational force due to the spheres of the larger ring would be zeroBThe net gravitational force due to the spheres of the smaller ring would be zeroCThe net gravitational force due to the spheres of both rings would be zeroDIf the smaller ring were removed, the mass would move towards the centre of the larger ring
If the position of the spheres approximates two uniformly dense rings, which of the following is the concerning a mass placed at position D?AThe net gravitational force due to the spheres of the larger ring would be zeroBThe net gravitational force due to the spheres of the smaller ring would be zeroCThe net gravitational force due to the spheres of both rings would be zeroDIf the smaller ring were removed, the mass would move towards the centre of the larger ringA uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionTwo rings having masses M and 2M respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
View SolutionTwo rings having masses M and 2M respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point P is
View SolutionA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
View SolutionA uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
View Solution
