Choose the most appropriate option.
If two simple pendulums first of bob mass M1 and length I1, second of bob mass M2 and l2. Given M1=M2 and l1=2l2. If the vibrational energies of both are same, then which of the following is correct?
Amplitude of B is smaller than A
Amplitude of B is greater than B
Amplitude will be same
None of the above
The correct Answer is:a
Similar Questions
Two simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
View SolutionTwo simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
View Solution
Knowledge Check
Two simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if these vibrational energy of both is same which is correct?
AAmplitude of B grater than ABAmplitude of B smaller than ACAmplitude will be sameDNone of theseA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
Atime period of pendulum is 2sBtension in the string is greater than mg cos15∘) at angualr displacement 15∘Crate of change of speed at angular displacement 15∘ is gsin15∘Dtension in the string is mg cos 15∘ at angular displacement 15∘The time period of a pendulum of length 'l' and mass of the bob 'm' is T. Time period of a pendulum with mass of the bob 2m and length l is ______.
ATB2TC3TD4T
A compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
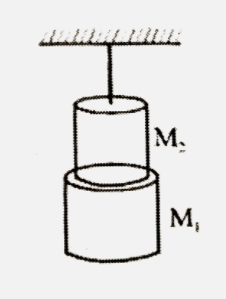
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-

View SolutionA simple pendulum of length 1 m with a bob of mass m swings with an angular amplitude 30∘. Then (g=9.8m/s2
View SolutionIf the inertial mass m1 of the bob of a simple pendulum of length 'l' is not equal to the gravitationalmassmg, then its period is
View Solution
