Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations.
Based on the above information, answer the following questions.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0.40),(20,40), (60, 20), (60, 0) The objective function is Z=4x+3y
Compare the quantity in Column A and Column B
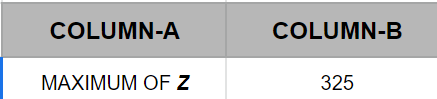
The quantity in column A is greater
The quantity in column B is greater
The two quantities are equal
The relationship cannot be determined on the basis of the information supplied
Step by step video solution for Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0.40),(20,40), (60, 20), (60, 0) The objective function is Z=4x+3y Compare the quantity in Column A and Column B by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
समान प्रश्न
The corner points of the feasible regon determined by the system of linear inequalities constrains are (0,0),(0,40),(20,40),(60,0). The objective function is z=4x+3y. Compare the quantity in column A and colum B.
01:40View SolutionFor an objective function Z=ax+by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
02:20View SolutionLinear programming is a method of finding the optimal value (maximum or minimum) when a relationship is expressed in the form of linear equations or inequalities. Solve the following linear programming problem graphically. Z=5x+3y Following is the constraint 3x+5yle15 5x+2yle10 And x,yge0 Answer the following questions on the basis of the above information. (iv)Z=5x+3y what will be the maximum value of
06:58View SolutionLinear programming is a method of finding the optimal value (maximum or minimum) when a relationship is expressed in the form of linear equations or inequalities. Solve the following linear programming problem graphically. Z=5x+3y Following is the constraint 3x+5yle15 5x+2yle10 And x,yge0 Answer the following questions on the basis of the above information. (v)Z=5x+3y what will be the minimum value of
06:58View SolutionLinear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The optimal value of the objective function is attained at the points
02:30View SolutionLinear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The graph of the inequality 3x + 4y < 12 is
04:10View SolutionLinear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The feasible region for an LPP is shown in the figure. Let Z = 2x + 5y be the objective function. Maximum of Z occurs at
02:26View SolutionLinear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5,5),(15,15),(0,20),let Z=px+qy, where p, q > 0 Condition on p and a so that the maximum of Z occurs at both the points (15,15) and (0,20) is
03:12View Solution

