O is the ortho centre of ΔABC and ∠BOC=120∘. Then ∠BAC is equal to
A
80∘
B
60∘
C
90∘
D
75∘
Text Solution
The correct Answer is:B
|
Similar Questions
Knowledge Check
Let O be the orthocentre of the triangle ABC. If ∠BOC=150∘, Then ∠BAC is
A30∘B60∘C90∘D120∘O is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
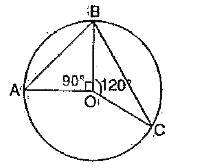 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘‘O' is the orthocentre of △ABC.Then ∠BOC+∠BAC is equal to:
O, △ABC में, △ABC का लंबकेंद्र है, तो ∠BOC+∠BAC कितना होगा?A120∘B135∘C180∘D90∘
In ΔABC,AC=BCand∠BAC=50∘. Find ∠BCA.
View SolutionO is the Ortho centre of ΔABC then A will be Orthocentre
View SolutionO is circumcentre of ΔABC if ∠BAC=85∘∠BCA=80∘ find ∠OAC.
View SolutionIn ΔABC , O is the circumcentre of the triangle and ∠BOC=60∘ , then what will be the value of ∠BAC ?
View SolutionIn the given figure O is the centre of the circle and ∠BAC=25∘, then the value of ∠ADB is :

View Solution
