O is orthocentre of ΔABC if ∠BOC=120∘ find ∠BAC
135∘
80∘
150∘
60∘
To solve the problem, we need to find the measure of angle BAC in triangle ABC, given that O is the orthocenter and angle BOC is 120 degrees.
1. Understanding the Orthocenter:
The orthocenter (O) of a triangle is the point where the three altitudes intersect. In triangle ABC, the altitudes from vertices A, B, and C meet at point O.
2. Identifying the Angles:
We know that angle BOC is given as 120 degrees. We need to find angle BAC.
3. Using the Relationship Between Angles:
In any triangle, the angles formed at the orthocenter have a specific relationship with the angles of the triangle. Specifically, the angle BOC can be expressed in terms of angle BAC:
∠BOC=180∘−∠BAC
4. Substituting the Known Value:
We substitute the known value of angle BOC into the equation:
120∘=180∘−∠BAC
5. Solving for Angle BAC:
Rearranging the equation to solve for angle BAC:
∠BAC=180∘−120∘
∠BAC=60∘
6. Conclusion:
Therefore, the measure of angle BAC is 60 degrees.
Final Answer:
∠BAC=60∘
The orthocenter (O) of a triangle is the point where the three altitudes intersect. In triangle ABC, the altitudes from vertices A, B, and C meet at point O.
We know that angle BOC is given as 120 degrees. We need to find angle BAC.
In any triangle, the angles formed at the orthocenter have a specific relationship with the angles of the triangle. Specifically, the angle BOC can be expressed in terms of angle BAC:
∠BOC=180∘−∠BAC
We substitute the known value of angle BOC into the equation:
120∘=180∘−∠BAC
Rearranging the equation to solve for angle BAC:
∠BAC=180∘−120∘
∠BAC=60∘
Therefore, the measure of angle BAC is 60 degrees.
∠BAC=60∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘Let O be the orthocentre of the triangle ABC. If ∠BOC=150∘, Then ∠BAC is
A30∘B60∘C90∘D120∘In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
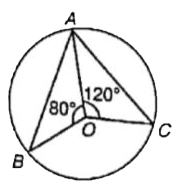 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the above
In ΔABC,AC=BCand∠BAC=50∘. Find ∠BCA.
View SolutionIf O is the orthocentre of a triangle ABC and ∠BOC=100∘, the measure of ∠BAC is
View SolutionIn given diagram Q is the circumcenter of ΔABC and O is the circumcenter of ΔBPC. If ∠BAC=65∘ then find the ∠OPC

View SolutionIn a ΔABC O is orthocentre ∠BOC=130∘ find ∠A ?
View SolutionO is the orthocentre of ΔABC, and if ∠BOC=110∘, then ∠BAC will be
View Solution
