O is circumcentre of ΔABC if ∠BAC=85∘∠BCA=80∘ find ∠OAC.
60∘
75∘
80∘
30∘
To solve for angle OAC in triangle ABC where O is the circumcenter, we can follow these steps:
Step 1: Identify the given angles
We are given:
- Angle BAC = 85°
- Angle BCA = 80°
Step 2: Calculate angle ABC
Using the property that the sum of angles in a triangle is 180°, we can find angle ABC:
Angle ABC=180°−Angle BAC−Angle BCA
Substituting the values:
Angle ABC=180°−85°−80°=15°
Step 3: Find angle COA
Since O is the circumcenter, angle COA is twice angle ABC:
Angle COA=2×Angle ABC=2×15°=30°
Step 4: Analyze triangle AOC
In triangle AOC, we know that AO = OC (as they are both radii of the circumcircle). Therefore, triangle AOC is isosceles, and we can denote:
- Angle OAC = Angle OCA = x
Step 5: Set up the equation for triangle AOC
The sum of angles in triangle AOC is 180°:
Angle OAC+Angle OCA+Angle COA=180°
Substituting the known values:
x+x+30°=180°
This simplifies to:
2x+30°=180°
Step 6: Solve for x
Subtract 30° from both sides:
2x=180°−30°=150°
Now divide by 2:
x=150°2=75°
Step 7: Conclusion
Thus, angle OAC = 75°.
Summary of the solution:
- Angle BAC = 85°
- Angle BCA = 80°
- Angle ABC = 15°
- Angle COA = 30°
- In triangle AOC, we found angle OAC = 75°.
We are given:
- Angle BAC = 85°
- Angle BCA = 80°
Using the property that the sum of angles in a triangle is 180°, we can find angle ABC:
Angle ABC=180°−Angle BAC−Angle BCA
Substituting the values:
Angle ABC=180°−85°−80°=15°
Since O is the circumcenter, angle COA is twice angle ABC:
Angle COA=2×Angle ABC=2×15°=30°
In triangle AOC, we know that AO = OC (as they are both radii of the circumcircle). Therefore, triangle AOC is isosceles, and we can denote:
- Angle OAC = Angle OCA = x
The sum of angles in triangle AOC is 180°:
Angle OAC+Angle OCA+Angle COA=180°
Substituting the known values:
x+x+30°=180°
This simplifies to:
2x+30°=180°
Subtract 30° from both sides:
2x=180°−30°=150°
Now divide by 2:
x=150°2=75°
Thus, angle OAC = 75°.
- Angle BAC = 85°
- Angle BCA = 80°
- Angle ABC = 15°
- Angle COA = 30°
- In triangle AOC, we found angle OAC = 75°.
Topper's Solved these Questions
Similar Questions
Knowledge Check
O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘O is the circumcentre of a triangle ABC. If ∠BAC=85∘and∠BCA=75∘ then what is the value of ∠OAC?
A40∘B60∘C70∘D90∘O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘
In a triangle ABC, O is the centre of incircle PQR, ∠BCA=75∘, find ∠ROQ :
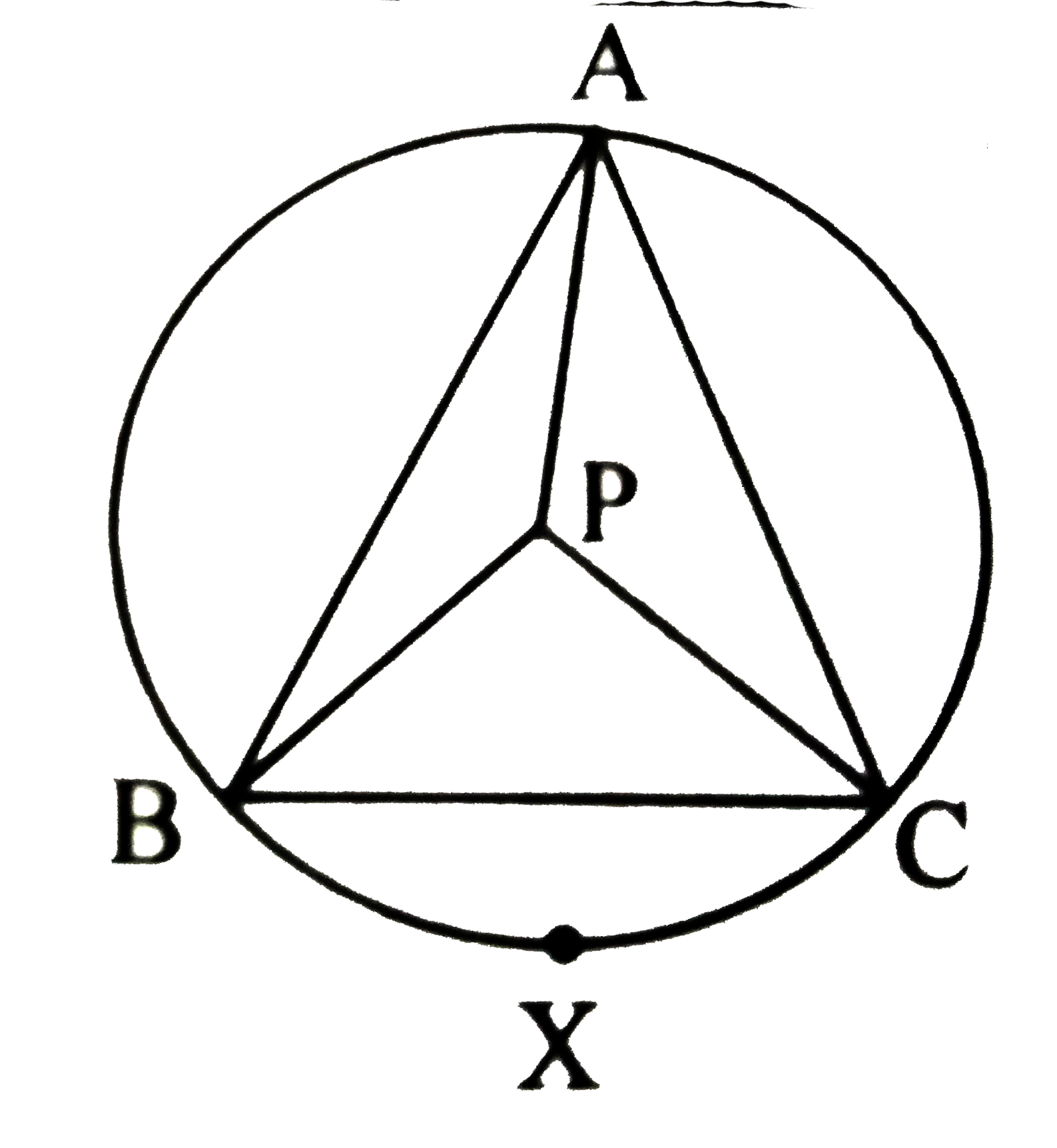
View SolutionIn the adjoining figure, P is the circumcentre of the ΔABC.m∠APC=118∘ and m∠PBC=45∘ , then find:
(i) m(arc BXC)
(ii) m(arc BCA)
View SolutionIn ΔABC,AC=BCand∠BAC=50∘. Find ∠BCA.
View SolutionIf S is the circumcentre of ΔABC and ∠A=50∘, then the value of ∠BCS is
View SolutionO is the circumcentre of the triangle ABC and ∠BAC=85∘, ∠BCA=75∘ , then the value of ∠OAC is
View Solution

