A rod of length L, along east-west direction is dropped from a height H. If B be the magnetic field due to Earth at that place and angle of dip is $θ,$ then the magnitude of the induced e.m.f. across two ends of the rod when the rod reachs the Earth is

A

$B L H cos θ$

B

$B L cos θ \times {(2 g H)}^{1 / 2}$

C

$B L cos θ / {(2 g H)}^{1 / 2}$

D

None of the above

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the magnitude of the induced e.m.f. across the ends of the rod when it reaches the Earth, we can follow these steps:
Step 1: Understand the scenario
A rod of length $L$ is dropped from a height $H$ in a magnetic field $B$ with an angle of dip $θ$ . The rod is oriented along the east-west direction.
Hint: Visualize the rod falling and the magnetic field lines acting on it.
Step 2: Determine the final velocity of the rod
When the rod is dropped from height $H$ , it will fall under the influence of gravity. The final velocity $v$ of the rod just before it reaches the ground can be calculated using the equation of motion:
$v = \sqrt{2 g H}$
where $g$ is the acceleration due to gravity.
Hint: Use the equation of motion that relates initial velocity, final velocity, acceleration, and distance.
Step 3: Find the horizontal component of the magnetic field
The magnetic field $B$ has a component in the direction of the rod's motion. Since the angle of dip is $θ$ , the horizontal component of the magnetic field $B_{h}$ is given by:
$B_{h} = B cos θ$
Hint: Remember that the angle of dip affects the orientation of the magnetic field.
Step 4: Calculate the induced e.m.f.
The induced e.m.f. $E$ across the ends of the rod can be calculated using the formula:
$E = B_{h} \cdot L \cdot v$
Substituting the values we have:
$E = (B cos θ) \cdot L \cdot \sqrt{2 g H}$
Hint: The induced e.m.f. is proportional to the length of the rod, the magnetic field component, and the velocity of the rod.
Step 5: Final expression for induced e.m.f.
Thus, the magnitude of the induced e.m.f. across the two ends of the rod when it reaches the Earth is:
$E = B L cos θ \sqrt{2 g H}$
Hint: Ensure to keep track of the units and the physical significance of each term in the equation.
Conclusion
The final answer is:
$E = B L cos θ \sqrt{2 g H}$

|

Updated on:8/8/2024

Class 12 PHYSICS MAGNETISM AND MATTER

Similar Questions

Knowledge Check

Question 1 - Select One
A vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is $θ$ . The induced e.m.f. in the rod is
A $B l v sin θ$
B $B l v tan θ$
C $B l v cot θ$
D $B l v cos θ$
Question 2 - Select One
A conducting rod of length $l$ falls verticaly under gravity in a region of uniform magnetic field $B$ . The field vectors are inclined at an angle $θ$ with the horizontal as shown in figure. If the instantaneous velocity of the rod is $v$ , the induced emf in the rod ab is

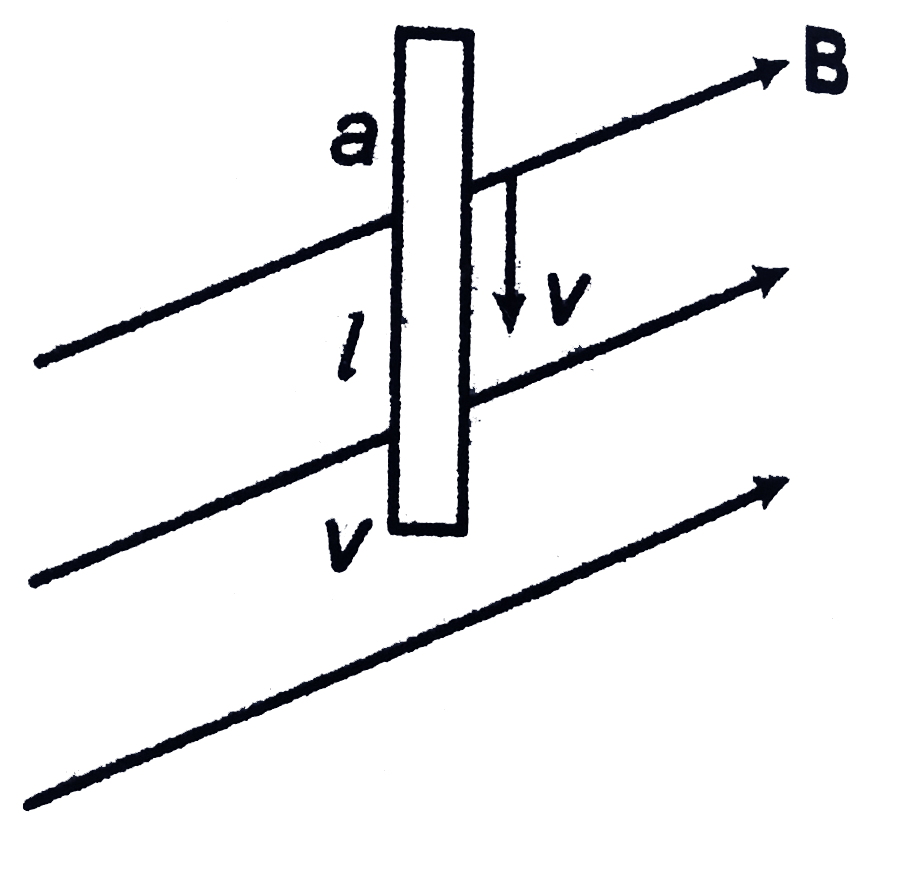A $B l v$
B $B l v cos θ$
C $B l v sin θ$
Dzero
Question 3 - Select One
A rod of length $L$ rotates in the form of a conical pendulum with an Angular velocity $ω$ about its axis as shown in Fig. 3.165. The rod makes an angle $θ$ with the axis. The magnitude of the motional emf developed across the two emf of the rod is

A(a) $\frac{1}{2} B ω L^{2}$
B(b) $\frac{1}{2} B ω L^{2} {tan}^{2} θ$
C( c) $\frac{1}{2} B ω L^{2} {cos}^{2} θ$
D(d) $\frac{1}{2} B ω L^{2} {sin}^{2} θ$

Recommended Questions

Home
Ask Doubt
Profile