A vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is θ. The induced e.m.f. in the rod is
Blvsinθ
Blvtanθ
Blvcotθ
Blvcosθ
The correct Answer is:C
To find the induced electromotive force (e.m.f.) in a vertical rod of length l moving with a constant velocity v towards the east in the presence of the Earth's magnetic field, we can follow these steps:
1. Understand the Setup:
- We have a vertical rod of length l moving towards the east with velocity v.
- The vertical component of the Earth's magnetic field is B, and the angle of dip is θ.
2. Identify the Components of the Magnetic Field:
- The Earth's magnetic field can be resolved into two components:
- The vertical component Bv=B (given).
- The horizontal component Bh can be found using the angle of dip θ.
- From trigonometry, we know:
tan(θ)=BvBh
- Rearranging gives:
Bh=Bvtan(θ)=Btan(θ)
3. Calculate the Induced e.m.f.:
- The formula for the induced e.m.f. (E) in a moving conductor in a magnetic field is given by:
E=Bh⋅l⋅v
- Substituting Bh:
E=(Btan(θ))⋅l⋅v
- This simplifies to:
E=B⋅l⋅vtan(θ)
4. Final Result:
- The induced e.m.f. in the rod is:
E=B⋅l⋅v⋅cot(θ)
Final Answer:
E=B⋅l⋅v⋅cot(θ)
---
- We have a vertical rod of length l moving towards the east with velocity v.
- The vertical component of the Earth's magnetic field is B, and the angle of dip is θ.
- The Earth's magnetic field can be resolved into two components:
- The vertical component Bv=B (given).
- The horizontal component Bh can be found using the angle of dip θ.
- From trigonometry, we know:
tan(θ)=BvBh
- Rearranging gives:
Bh=Bvtan(θ)=Btan(θ)
- The formula for the induced e.m.f. (E) in a moving conductor in a magnetic field is given by:
E=Bh⋅l⋅v
- Substituting Bh:
E=(Btan(θ))⋅l⋅v
- This simplifies to:
E=B⋅l⋅vtan(θ)
- The induced e.m.f. in the rod is:
E=B⋅l⋅v⋅cot(θ)
E=B⋅l⋅v⋅cot(θ)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)30videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - J)4videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION -J(Aakash Challengers Questions)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The vertical component of earth's magnetic field is zero at a place where angle of dip is :
A0∘B45∘C60∘D90∘ - Question 2 - Select One
The vertical component of earth's magnetic field is zero at a place where anlge of dip is
A0∘B45∘C60∘D90∘ - Question 3 - Select One
At a place, horizontal and vertical components of earth's magnetic field are equal. Angle of dip at the given place is
A30∘B90∘C45∘D0∘
Horizontal and vertical components of earth’s magnetic field at a place are equal. The angle of dip at that place is ________.
View SolutionAt a particular place, horizontal and vertical components of earth's magnetic field are equal. The angle of dip at that place is…………… .
View SolutionA rod of length b moves with a constant velocity v in the magnetic field of a straight long conductor that carries a current I as shown in the below figure. The emf induced in the rod is
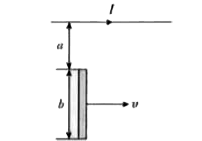 View Solution
View SolutionAt a particular place, horizontal and vertical components of earth's magnetic field are equal. The angle of dip at that place is…………… .
View SolutionA uniform circular metal disc of radius R is rotating about a vertical axis passing through its centre and perpendicular to its plane with constant frequency f. If BH and BV are horizontal and vertical components of the Earth's magnetic field respectively, then the induced e.m.f between its centre and the rim is
View Solution

