45 people take 18 days to dig a pond. If the pond would have to be dug in 15 days, then the number of people to be employed will be :
50
54
60
72
To solve the problem, we can use the concept of work done, which is based on the formula:
Work=Number of People×Number of Days
Given that 45 people take 18 days to dig a pond, we can first calculate the total work done in terms of "person-days".
Step 1: Calculate the total work in person-days
Total Work=45 people×18 days=810 person-days
Step 2: Determine the number of people required to complete the same work in 15 days
Let x be the number of people required to complete the work in 15 days. The equation for the work done in this case will be:
Total Work=x people×15 days
Step 3: Set the two expressions for work equal to each other
810 person-days=x people×15 days
Step 4: Solve for x
To find x, we can rearrange the equation:
x=810 person-days15 days=54 people
Conclusion
Thus, the number of people required to dig the pond in 15 days is 54.
---
Total Work=45 people×18 days=810 person-days
Let x be the number of people required to complete the work in 15 days. The equation for the work done in this case will be:
Total Work=x people×15 days
810 person-days=x people×15 days
To find x, we can rearrange the equation:
x=810 person-days15 days=54 people
Thus, the number of people required to dig the pond in 15 days is 54.
Similar Questions
Knowledge Check
Six people i.e. Q, W, K, U, R and L have meeting on different days of the same week starting from Monday and ends on Saturday. K has meeting just after Q but not on Thursday. Not more than two people have meeting after R. Three people have meeting between R and W. The number of people have meeting after W is same as the number of people have meeting before U. How many people have meeting before L?
ATwoBOneCThreeDFourA contractor undertook to do a piece of work in 9 days. He employed certain number of laboures but 6 of them were absent from the very first day and the rest could finish the work in only 15 days. Find the number of men originally employed
A15B6C13D9A contractor undertook to do a certain piece of work in 18 days. He employed certain number of men but 12 of them being absent from the very 1st day , the rest could finish the work in 30 days . Find the number of men originally employed .
A40B15C45D30
The following table gives zonewise survey report of the people of a country who take coffee. Study the table and answer the questions.
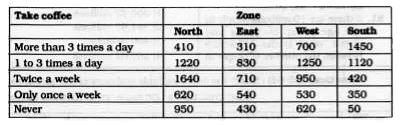
The ratio of the total number of people surveyed who take coffee more than 3 times a day to the total number of people who do not take coffee at all is
View Solution450 man-days of work can be completed by a certain number of men in some days. If the number of people (men) are increased by 27, then the. number of day required to complete the same work is decreased- by 15. The number of days are required to complete the" three times work (than the previous/actual work) by 27 men?
View Solution450 man-days of work can be completed by a certain number of men in some days. If the number of people (men) are increased by 27, then the. number of day required to complete the same work is decreased- by 15. The number of days are required to complete the" three times work (than the previous/actual work) by 27 men?
View SolutionTheere are 4 people whow can complete a work in 19 days. Individually. The work is started by one of people on the first day. Everyday one more person joins and starting from the 4th days, all of the 4 people work be completed?
View SolutionA contractor undertook to do a piece of work in 9 days. He employed certain number of laboures but 6 of them were absent from the very first day and the rest could finish the work in only 15 days. Find the number of men originally employed
View Solution
