ABCD is a parallelogram and line segments AX,CY bisects the angles A and C respectively show that AX||CY.Solution in Punjabi
Step by step video & image solution for ABCD is a parallelogram and line segments AX,CY bisects the angles A and C respectively show that AX||CY. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three angles of a quadrilteral are respectively 50∘ and 110∘ and 100∘ . Find the fourth angles.
View SolutionDefine a trial.
View SolutionDefine
Statistics as a subject.
View SolutionABCD is a parallelogram andline segments AX,CY bisect the angles A and C, respectively Figure. Show that AXCY. Figure
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionABCD एक समान्तर चतुर्भुज तथा रेखा AX तथा CY क्रमशः कोणों A तथा C का समद्विभाजन करती है। सिद्ध कीजिए किAX∣∣CY
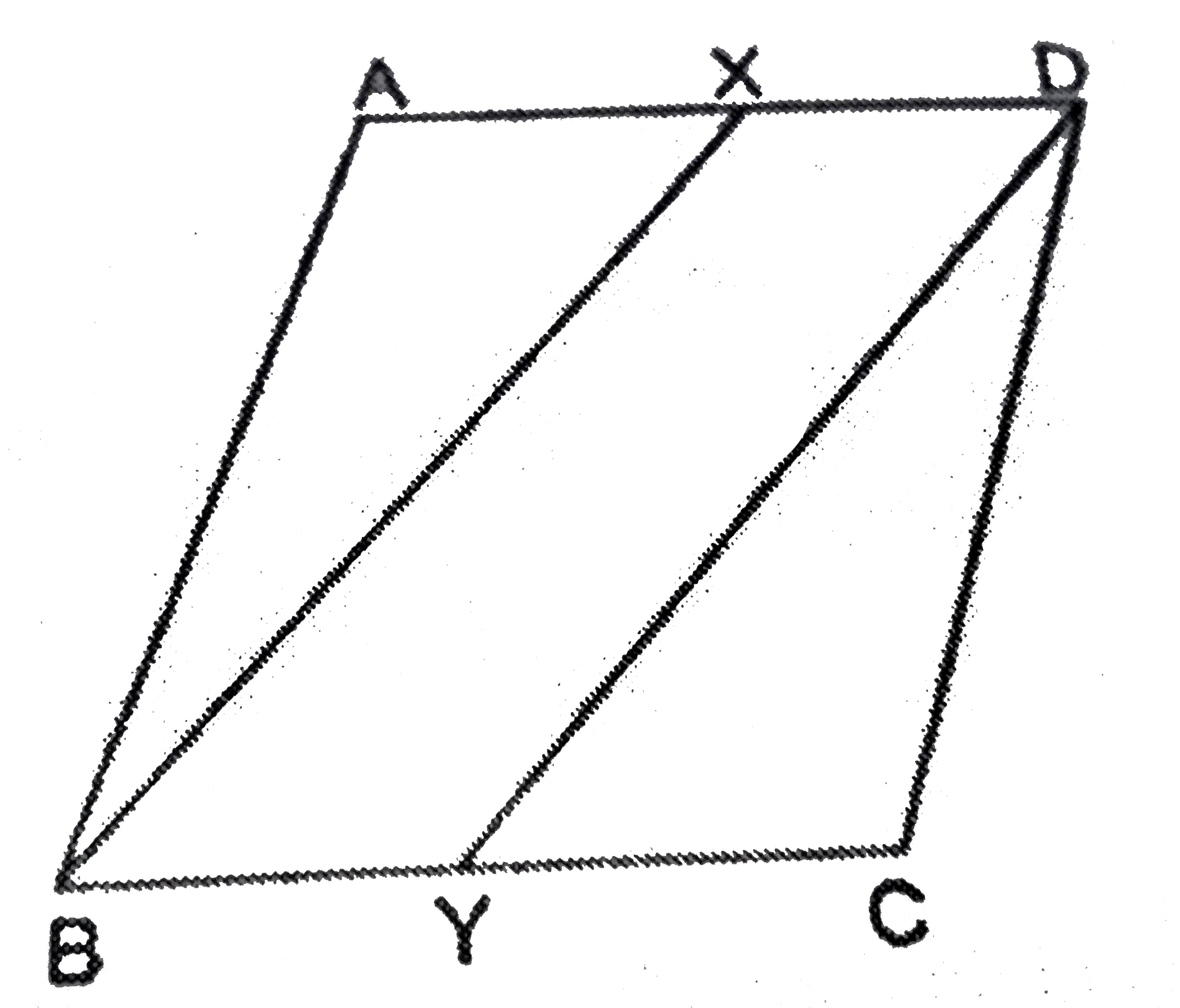
View Solutionचित्र में ABCD एक समांतर चतुर्भुज है और X,Y क्रमशः भुजाओं AD और BC पर इस प्रकार है कि AX=14AD और CY=14BC। दिखाइए कि □XBYD एक समांतर चतुर्भुज है।
View Solutionसाबित करे कि
∣∣ ∣ ∣∣abax+bybcbx+cyax+bybx+cy0∣∣ ∣ ∣∣=(b2−ac)(ax2+2bxy+cy2)
View Solutionसारणिकों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए - ∣∣ ∣ ∣∣abax+bybcbx+cyax+bybx+cy0∣∣ ∣ ∣∣=(b2−ac)(ax2+2bxy+cy2)
View Solution∣∣ ∣ ∣∣abax+bybcbx+cyax+bybx+cy0∣∣ ∣ ∣∣=(b2−ac)(ax2+2bxy+cy2)
View SolutionOne of the lines represented by the equation ax2+bxy+cy2=0 bisects an angle between the co-ordinate axes
View Solution|(a,b,ax+by),(b,c,bx+cy),(ax+by,bx+cy,0)|=
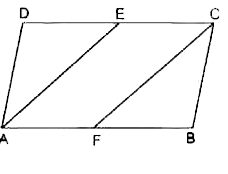
View SolutionIn the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
View SolutionIf a,b,c are in G.P then the value of the determinant Δ=⎡⎢⎣abax+bybcbx+cyax+bybx+cy0⎤⎥⎦ is
View SolutionIn the figure, AX and CY are bisectors of angles A and C in front of the parallelogram ABCD, respectively. Show that AX ||CY is.
View SolutionIf ∣∣ ∣ ∣∣abax+bybcbx+cyax+bybx+cy0∣∣ ∣ ∣∣=0andax2+2abxy+cy2≠0, then ......
View Solution
