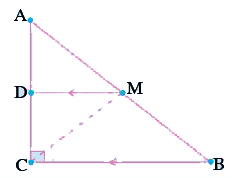
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = 12AB .Solution in Punjabi
Step by step video & image solution for ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = 1/2 AB . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three angles of a quadrilteral are respectively 50∘ and 110∘ and 100∘ . Find the fourth angles.
View SolutionDefine a trial.
View SolutionDefine
Statistics as a subject.
View SolutionABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD⊥AC
(iii) CM = MA=12AB
View SolutionABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य - बिंदु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D भुजा AC का मध्य - बिंदु है। (ii ) MD⊥AC है
(iii) CM=MA=12AB है।
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid-point of AC
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
MD⊥AC
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
CM=MA=12AB
View SolutionABC is a triangle right angled at C. A line through the mid points M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid point of AC
MD⊥AC
CM=MA=12AB
View SolutionABC is a right angle in a right triangle ABC. If the line drawn parallel to BC through the hypotenuse AB denominator M intersects AC at D, then prove the following point AC midpoint D
View SolutionABC is a right angle in a right triangle ABC. Prove the following if the line drawn parallel to BC through the midpoint M of hypotenuse AB intersects AC at D. CM=MA = 1/2 AB
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
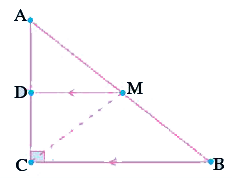
View SolutionABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that
(i) D is the midpoint of AC
(ii) MD⊥AC
(iii) CM=MA=12AB.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM=MA=12AB
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View Solution
