ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that: ar(BPC) = ar(DPQ)Solution in Punjabi
Step by step video & image solution for ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that: ar(BPC) = ar(DPQ) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
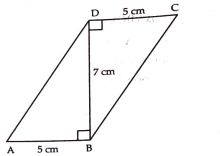 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionP और Q क्रमश : समांतर चतुर्भुज ABCD कि भुजाओ में DC और AD पर स्थित बिंदु है । दर्शाइए कि ar(APB)=ar(BQC) है |
View Solutionआकृति में, ABCD एक समांतर चतुर्भुज हैं और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया हैं कि AD=CQ हैं । यदि AQ भुजा DC को P पर प्रतिच्छेद करती हैं , तो दर्शाइए कि ar(BPC)=ar(DPQ) हैं |
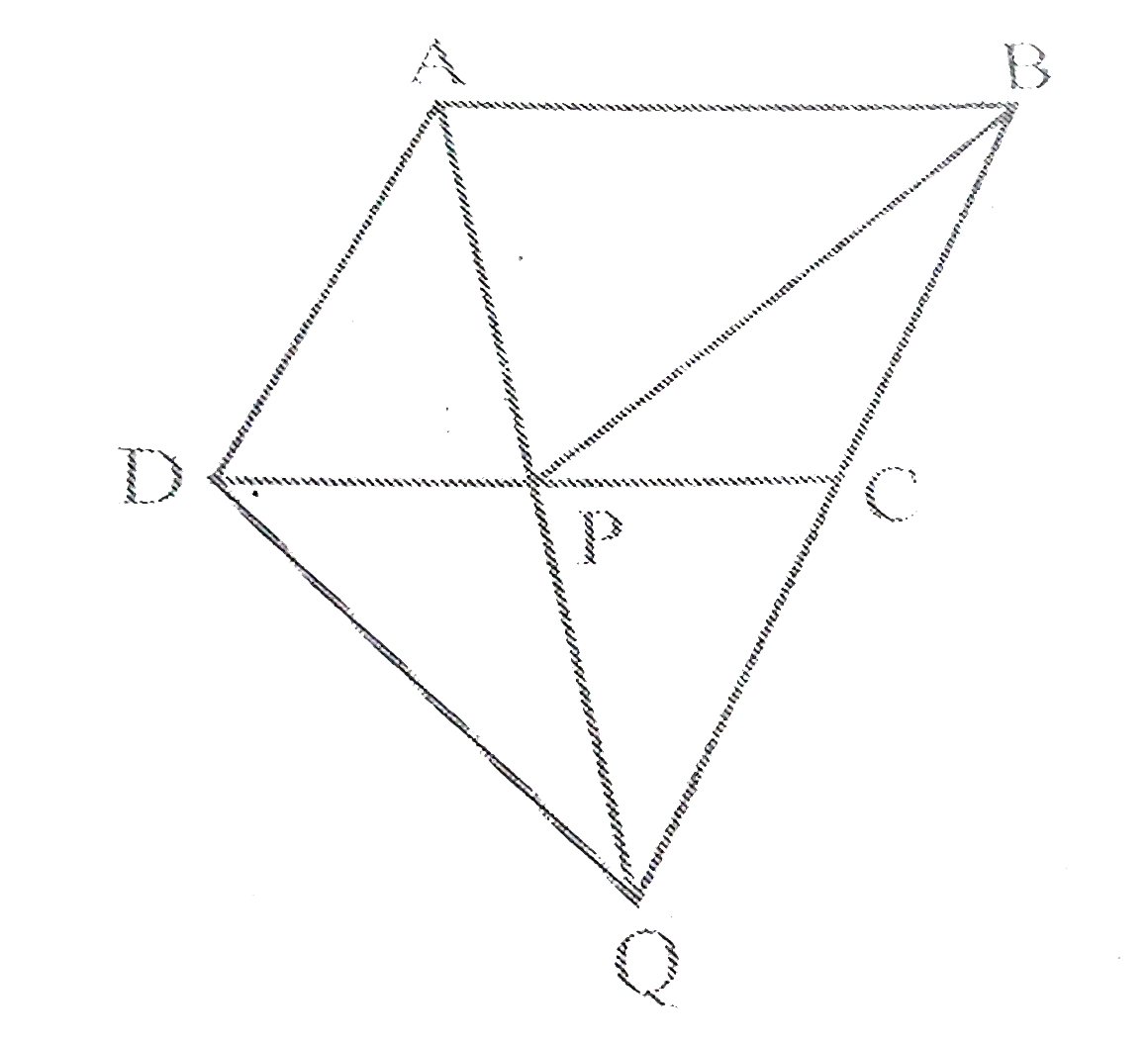
View SolutionP और Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर बिन्दु है। दर्शाइए कि ar (APB) = ar (BQC) है।
View Solutionआकृति में ABCD एक समांतर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD=CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है तो दर्शाइए कि ar (BPC) = ar (DPQ) है।
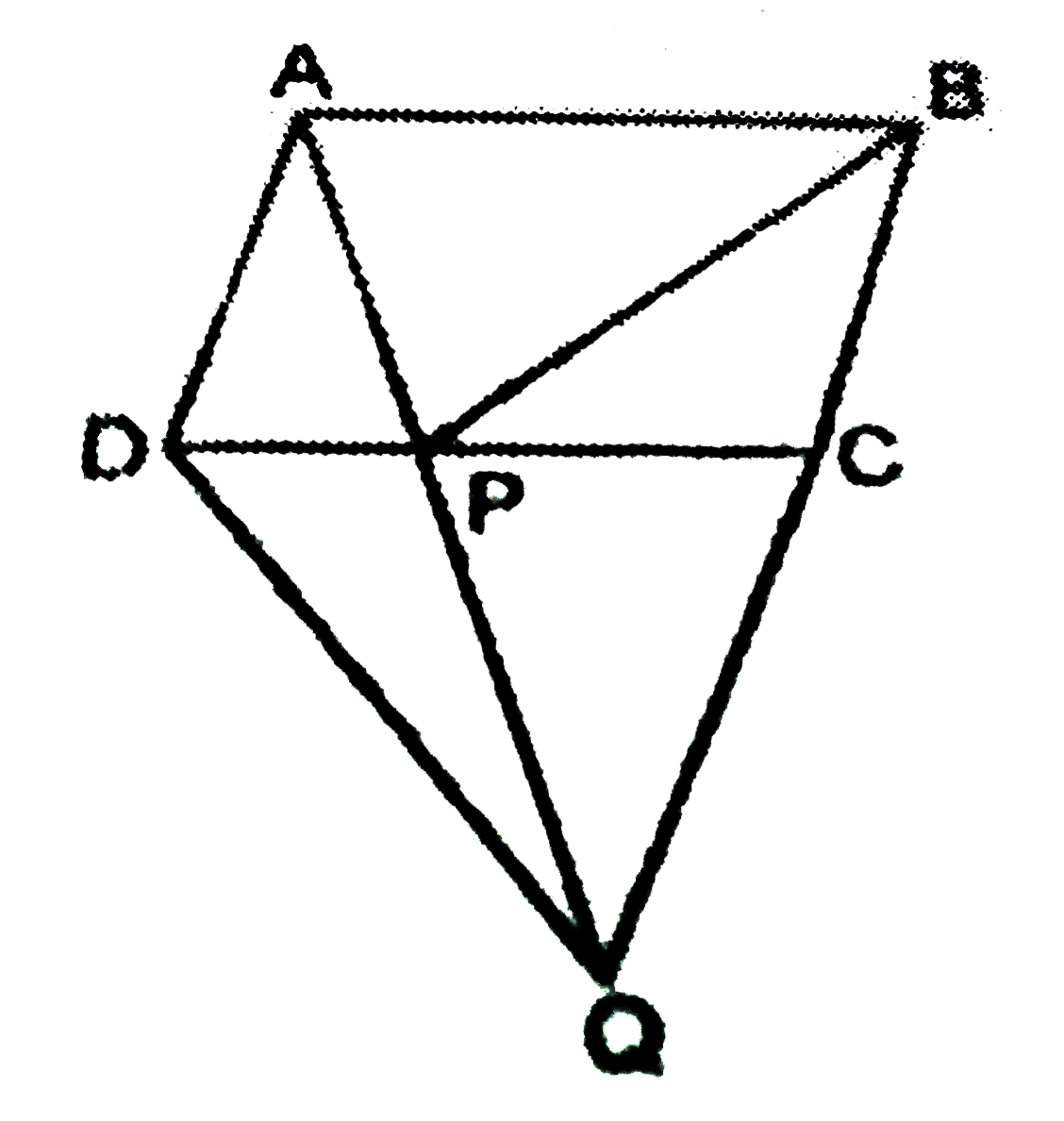
View Solutionदिए गए चित्र में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है की AD = CQ है|यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए की ar(BPC)=ar(DPQ)
View SolutionP और Q किसी समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित दो बिंदु है |दिखाएँ की ar(ΔAPB)=ar(ΔBQC)
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram , ABCD . Show that ar(APB) = ar (BQC)
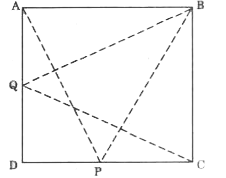
View SolutionIn the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect AD = CQ. If AQ intersect DC at P, Show that ar (BPC) = ar (DPQ)
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD show that ar(ΔAPB)=arΔ(BQC)
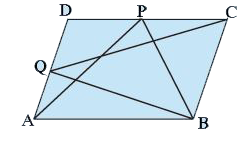
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD show that ar(ΔAPB)=arΔ(BQC)
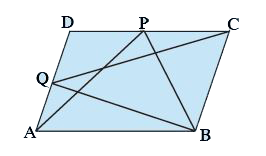
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD show that ar(ΔAPB)=arΔ(BQC)
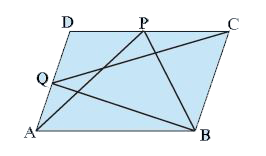
View SolutionABCD is a parallelogram and BC is extended to Q in such a way that AD=CQ is. If the AQ arm intersects DC at P, then show that ar(BPC)=ar(DPQ)
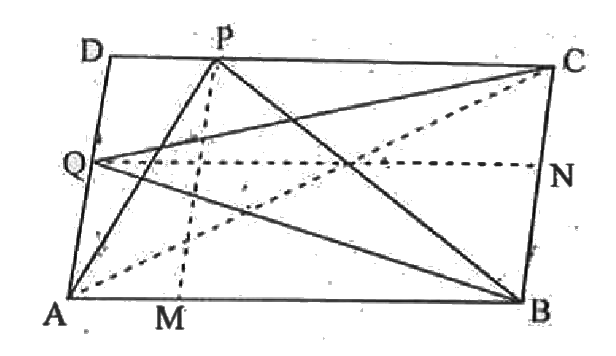
View SolutionIn the figure, ABCD is a parallelogram. The points P and Q divide the side BC into three equal parts. Prove that ar(APQ)=ar(DPQ)=(1)/(6)ar(ABCD) is.
View Solution
