Two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that ar(∣∣gmABCD) + ar(∣∣gmAEFB) = ar(∣∣gmEFCD)Solution in Punjabi
Step by step video & image solution for Two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that ar(||gmABCD) + ar(||gmAEFB) = ar(||gm EFCD) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
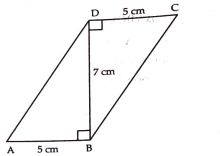Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
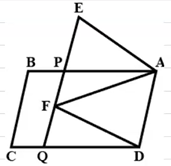
View Solutionआक्रति 9.13 में , ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है ।
साथ ही , AL⊥DC है सिद्ध कीजिए कि
(i) ar(ABCD)=ar(EFCD)
(ii)(ABCD)=DC×AL
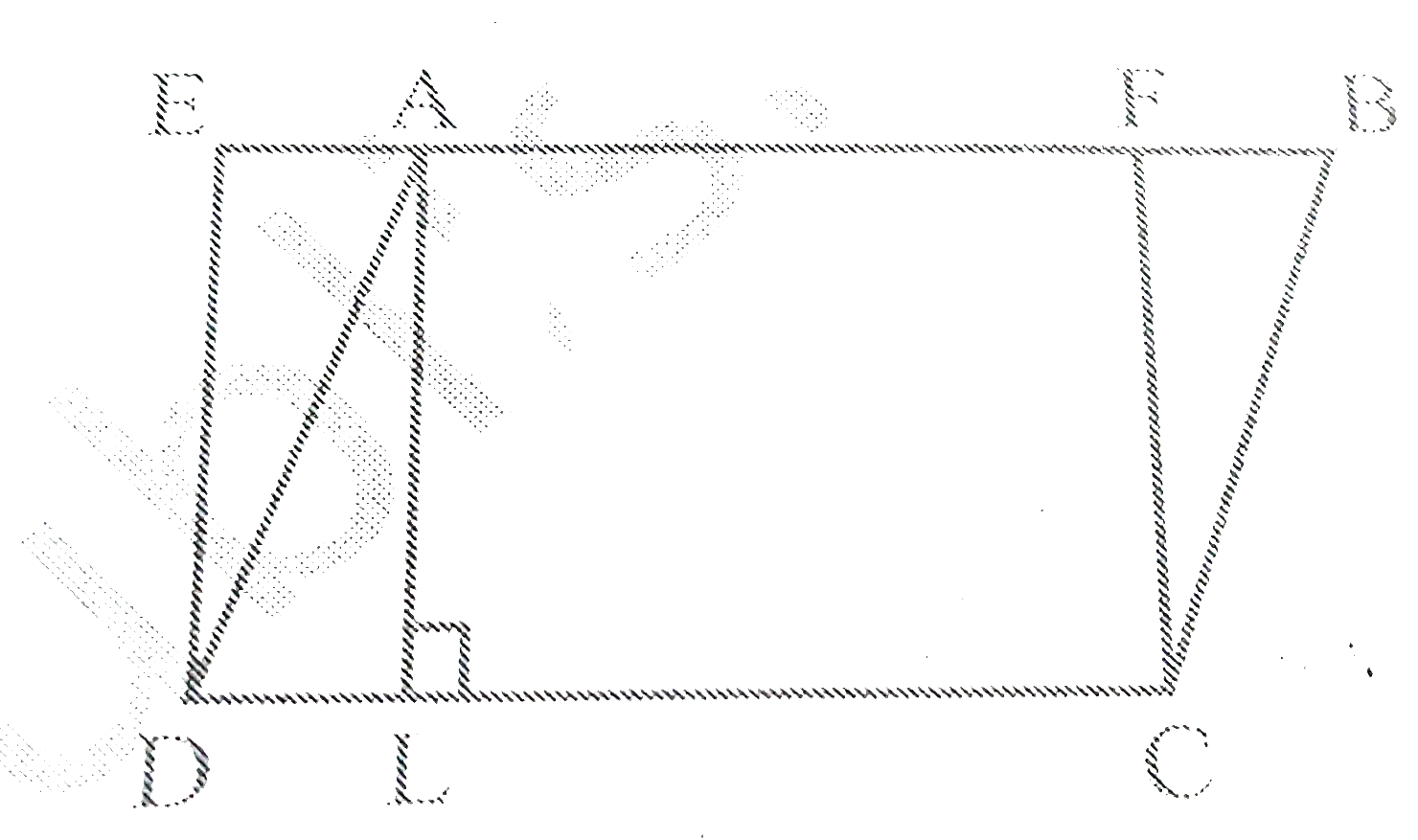
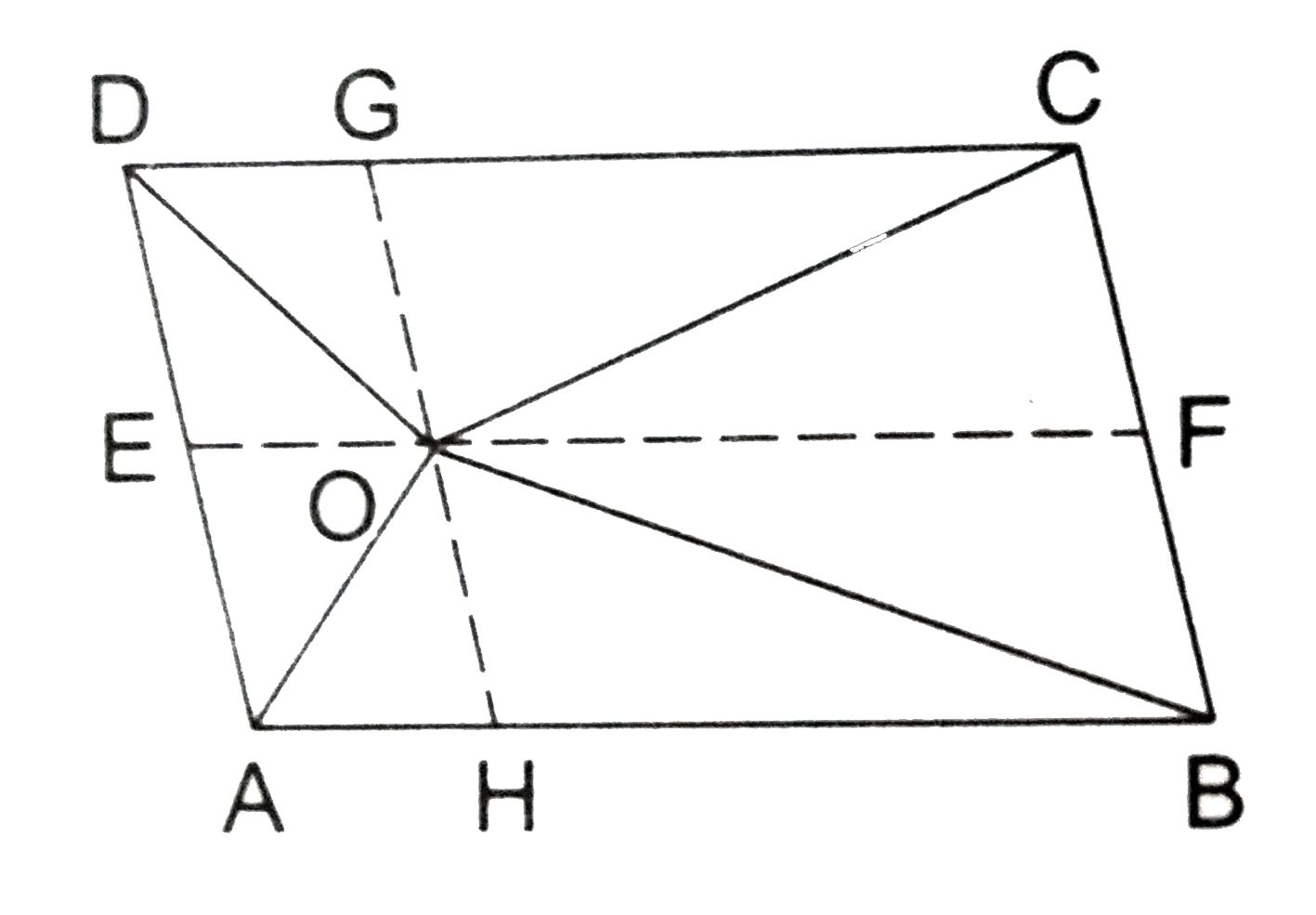
View SolutionABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
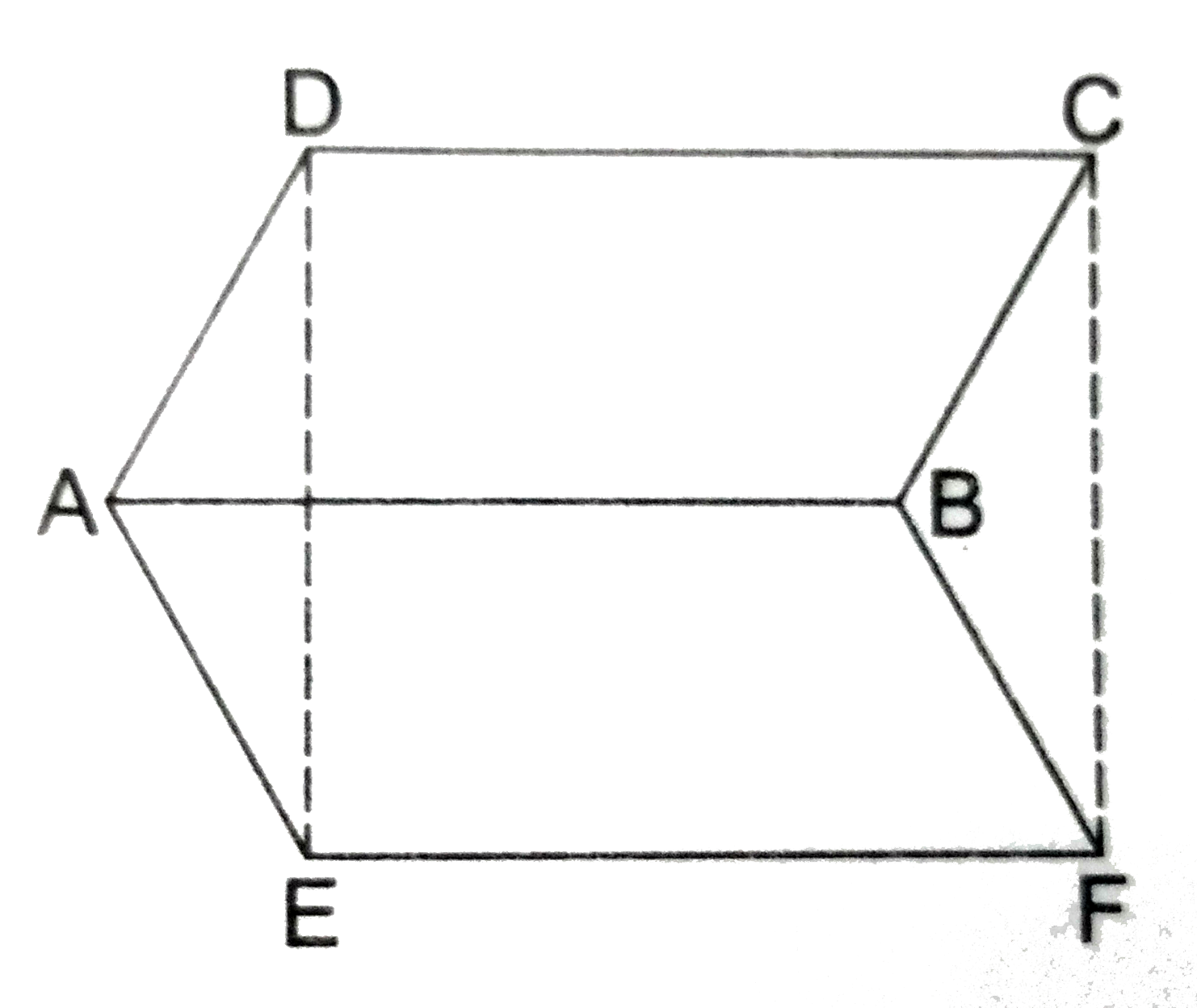
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL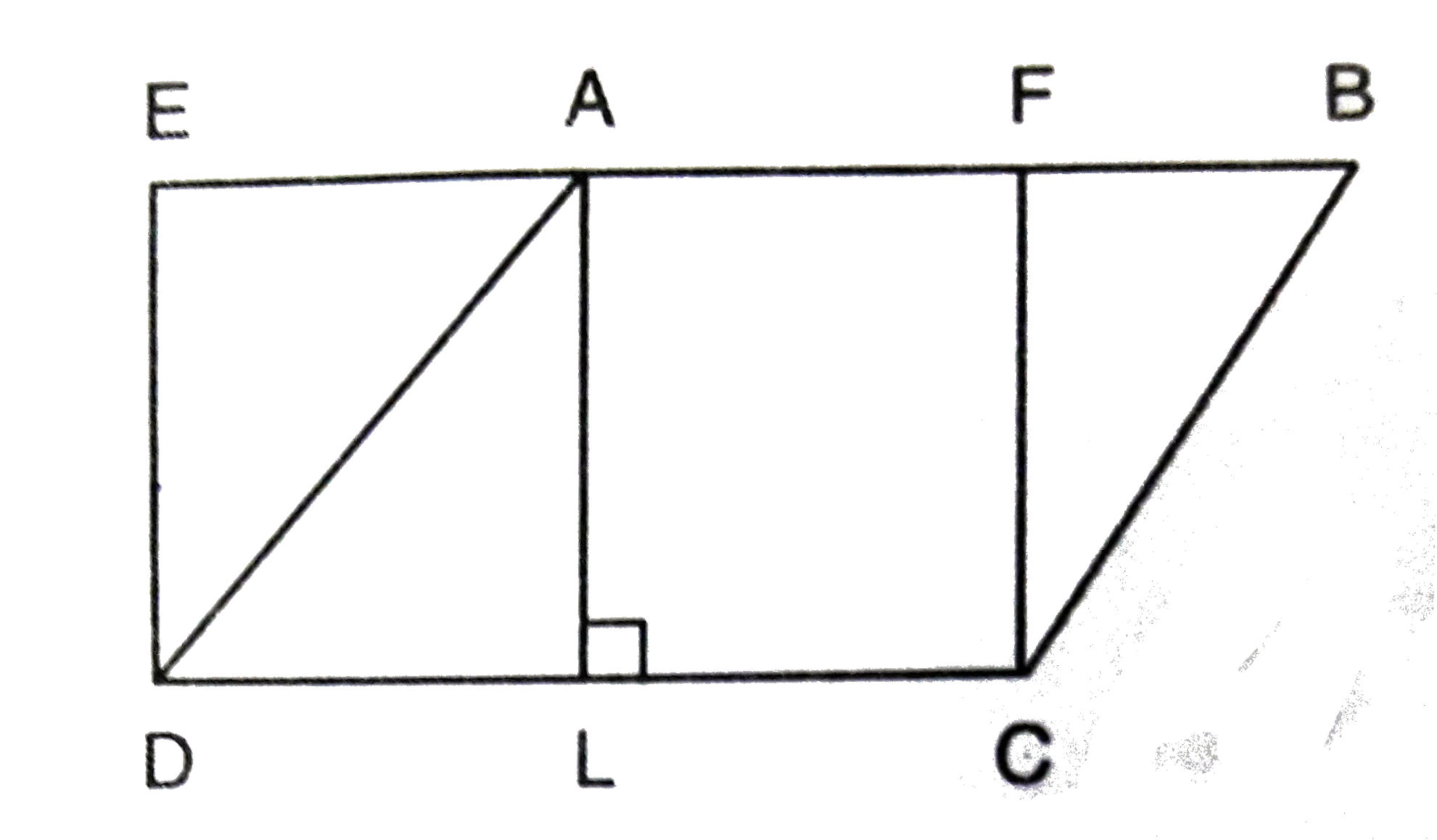
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View Solutionसमांतर चतुर्भुज ABCD की भुजा AB को किसी बिंदु P तक बढ़ाया गया है। बिंदु A से CP के समांतर खींची गयी रेखा CB के आगे बढ़ाये गये भाग को Q पर मिलती है। और समांतर चतुर्भुज PBQR को पूरा करती है। सिद्ध कीजिए कि
ar(।।gmABCD)=ar(।।gmBPRQ)
View Solutionसमांतर चतुर्भुज ABCD में भुजाओं AB तथा BC पर कोई दो बिंदु क्रमशः E तथा F है, सिद्ध कीजिए कि ar(ΔADF)=ar(ΔDCE).
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View Solution